Проверка результатов A/B теста
A/B-тесты это основной способ решения споров об интерфейсах в команде. Но часто эти споры решаются неверно, потому что ключевая ошибка при анализе результатов A/B теста это сравнение двух средних, без подбора критерия, оценки выборки. Беглый визуальный анализ отчетов в GA по принципу «где график выше, та версия и лучше» приводит к ошибочным выводам и стоит бизнесу кучу денег. Если до этого момента вы обходились знаниями, что онлайн-калькуляторы должны показать «p < 0.05» и «нормальное распределение похоже на колокол», то в этой статье я постараюсь расширить ваш кругозор.
Все примеры будут продемонстрированы для R-Studio. Общий процесс анализа: экспериментальный дизайн → сырые данные → обработанные данные → выбор статистической модели → суммарная статистика → p value. С экспериментальным дизайном дизайнеры справляются, про остальные шаги давайте говорить подробнее.
Формируем гипотезу
При формировании гипотезы руководствоваться лучше простыми понятиями: цели бизнеса, как эти цели достигаются клиентами и как это можно измерить (Single A/B test или Multi A/B test). Не менее важно понимать, как данные будут собираться и валидироваться, и как будут вноситься изменения по результатам теста. При этом предполагается, что проблема репрезентативности и достаточности объёма выборки решена. По умолчанию в данном уроке мы будем считать, что стандартное отклонение (корень из дисперсии) не зависит от размера выборки, так как выборка репрезентативна.
Но будем честны, часто задача будет ставиться по принципу: «у нас упала прибыль, посмотри, че там такое». Или приходит продукт-менеджер или гейм-дизайнер, рассказывает про уже реализованную фичу на проде, и просит узнать эффективность этой фичи. При этом нет информации, на что эта фича была направлена, на каких данных ее исследовать, как ее операционализировать. В случае столь слабо формализованных задач нужно придумывать гипотезы самостоятельно и думать, откуда взять данные для формирования этих гипотез. Помогает консолидация данных из разных источников.
Либо, в качестве источника гипотезы банальный спор менеджеров продукта и проекта, результат коридорного опроса, желание оптимизировать CRO. Я не люблю тестировать фичи, которые очевидно улучшат конверсию, это достаточно бесполезная работа. Лучше тестировать фичи, у которых отдача бизнесу непредсказуема. В таких фичах обычно кроется рост всех ключевых метрик: CTR (Click Through Rate), конверсия, CPA, ROAS, CPI. Должен сказать, что при малом количестве данных очень сложно оценивать небинарные метрики (средний чек, выручка), результаты обычно очень шумные: работает принцип garbage in garbage out. А вот A/B тесты для бинарных задач проводить просто (выполнено/не выполнено). Но в любом случае самый первый шаг это определиться с целевой метрикой.
Далее мы должны определиться с математикой. Например, у нас частотный подход, а не Байес. Выбираем класс критериев. Если распределение нормальное, то параметрические критерии (Стьюдент, Anova для равенства средних; F-test, Бартлетта, Левана на равенство дисперсий; тест пропорций для биномиальных метрик; формальные тесты на принадлежность распределению). Они считают свою статистику на основе информации об оригинальной функции распределения, т.е. мы должны задать некие переменные. Если сравниваем средние и данных не много, то Bootstrap (траты внутри приложения). Последняя инстанция это непараметрические тесты, им нужна только информация из выборки. Есть подклассы: критерии случайности, симметрии, корреляции, сдвига и масштаба, сдвига. Они не такие мощные, но применимы везде. Так, Манна-Уитни и Краскала-Уоллисана наличие сдвига, для зависимых выборок тест Фридмана и «знаковый» критерий Уилкоксона, Bootstrap для сравнения распределения характеристик по квантилям и хи-квадрат Пирсона для изменения функций распределения.
Отличная практика для реальных данных со смещением влево, это сравнить две выборки непараметрикой, и сравнить эти же выборки после логарифма t-test’ом. Двойная проверка результата.
Хорошая гипотеза учитывает принципы индукции и фальсифицируемости. Индукция это отрицание гипотезы, возможность сформулировать негативного суждения. Древнегреческие боги были? Нет, не было. Фальсифицируемость же про попытки опровергнуть гипотезу, и если не получилось, тогда гипотезу можно принять. Докажи что не было Древнегреческих богов, а до тех пор считаем, что они были.
При проверке гипотезы помним, что нулевая гипотеза про отсутствие отличий, для ее доказательства нужна вся популяция, а не выборка. Альтернативная гипотеза говорит о значимости различий. Все отличия в выборках это всегда альтернативная гипотеза, а проверяется всегда нулевая. Ошибка первого рода (α, false positive) происходит, когда мы отклоняем нулевую гипотезу в пользу альтернативной гипотезы, при условии что справедлива нулевая гипотеза. H0 считается верной, пока не доказано обратное, и если она отвергается, значит нам пора бежать предпринимать действия. Это та самая альфа 0,05, которая говорит что в одном случае из 20 будет ошибка первого рода. Ошибка второго рода (false negative) происходит, когда верна альтернативная гипотеза, но было принято решение принять нулевую гипотезу. Другими словами, во время дизайна теста мы задаем уровень значимости. который показывает вероятность верности нулевой гипотезы. На основе significance level мы принимаем или отвергаем гипотезу с полученным p-value, это вероятность совершить ошибку первого рода. Вероятность ошибки второго рода это 1 — power, шанс не заметить значимые изменения. Поэтому нет смысла делать дизайна тестов базируясь только на ошибке первого рода. Низкое значение уровня значимости уменьшает шанс совершить ошибку первого рода, но растет шанс совершить ошибку второго рода, поэтому значение p-value подбирается исходя из критичности допуска ошибок. Например, нельзя допустить ошибку второго рода в таком кейсе: не сработать сигнализацией при попытке угона машины, это критично. При работе с калькуляторами вроде evanmiller для расчёта доверительных интервалов разницы мы не учитываем ошибку второго рода.
Возможно, некоторым будет проще понять так: p-value это соответствие площадей двух гипотез, дисперсии равны.
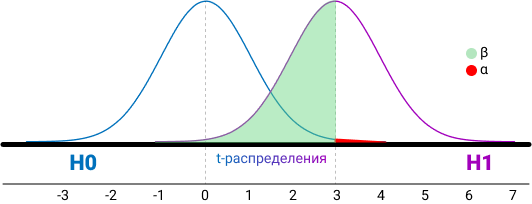
Доверительные интервалы всегда считаются по результатам теста и куда информативнее, чем размер выборки и мощность. Доверительные интервалы это способ смотреть на соответствие реальных и теоретических данных. Выборка из нормального распределения, и выборочное среднее не может быть равно мат. ожиданию. Поэтому нам нужно знать интервал, в который попадает значение оцениваемого параметра.
Итак, summary: если человек болен и мы это подтвердили — true positive (TP). Если человек не болен и мы это подтвердили — true negative (TN). Ошибка первого рода — здоровому человеку сказали, что он болен (FP). Или ошибка второго рода, сказали больному человеку что он здоров (FN).
Ошибки будут всегда, и для определения их существенности есть две метрики: полнота и точность (recall и precision), они про количество ошибок первого и второго рода. Recall = TP/(TP+FN), Precision = TP/(TP+FP). Метрики между собой конкурируют, поэтому надо учитывать обе метрики по интегральной характеристике.
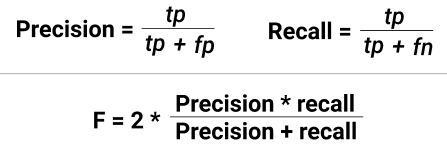
И вернемся к метрикам бизнеса, нельзя про них забывать в ходе погружения в техническую часть. Надо видеть картину целиком. Если игнорировать LTV (lifetime value или сколько денег принес клиент за свой жизненный цикл) и ROI (return on investment или окупилась ли сумма привлечения клиента), то в краткосрочной перспективе можно хорошо поднять метрики ARPU diary, ARPU month и процент платящих, чем часто пользуются продуктовые менеджеры, бегающие из компании в компанию. Для краткосрочного поднятия ARPU достаточно ввести дополнительные регулярные акции. Но в долгосрочной перспективе такой подход приведет к финансовым проблемам, так как каннибализирует остальные механики привлечения денег, и это будет видно на LTV 6 month. Еще можно выполнить краткосрочный KPI если uplift-нуть CTR одной кнопки, и каннибализировать CTR других кнопок. Или остановить трафик для мобильного приложения, очень краткосрочно подрастет ROI. В общем, любые временные изменения в базовой экономике всегда ведут к временному увеличению метрик с дальнейшей трагической просадкой. Можно привести более наглядный пример: промо-ловушка из продуктовых магазинов. Покупатель думает, что цены растут и доходы снижаются, значит нужно меньше тратить. Продавцы это видят и снижают цены в рамках акций, это увеличивает выручку на короткий промежуток времени. Покупатели привыкают к акциям и идут в магазин целенаправленно в поисках товаров по скидке, продавец вынужден еще раз снижать цену, и далее делать это постоянно. При чем тут тесты? Бизнес после запуска разовой акции видит, что прибыль пошла вверх, трафик увеличился, клиентов стало больше, но вы как аналитик должны сказать, что не смотря на это выгода/маржа/грязный вал в разрезе трех месяцев упали. Это вечная дилема: выполнить план и получить просадку по марже, или не выполнить план, разово увеличить прибыль, но просесть по выручке. Говорите бизнесу про положительную EBITDA, тогда они вас будут слушать
Я буду приводить p-value = 0,05, так как это общепринятое значение. В реальных проектах p-value куда меньше.
Запуск A/B теста и сбор данных
Либо вы идете к разработчику и он каким то образом все делает за вас, и при работе с мобилками это основной способ проведения A/B теста. Либо используете GTM или Google Optimize, где разделяем трафик, готовите визуальное представление гипотезы и задаете условия ее отображения (сегменты и тому подобное). В результате будет возможность менять не только цвет и тексты на странице, но и создавать новые функциональные сущности или развивать имеющиеся, а также успешно сегментировать гипотезы еще на этапе запуска. Это дает большое преимущество в условиях ограниченных технических и финансовых ресурсов крупного бизнеса.
С Optimize надо быть осторожным, нельзя полагаться на автоматику. Так, предположим что у вас есть два варианта страницы, но только второй вариант проходит через переадресацию. Тогда latency и частота отказов у второго варианта будет больше, как следствие, когорта меньше. Если смотреть более глобально на вопрос «в какой момент пользователь должен попасть в свою группу во время теста», то очевидным ответом будет «чем раньше, тем лучше». Тесты могут быть exposed и non-exposed, в первом случае мы сталкиваем пользователя с изменениями на сайте и тем самым уменьшаем дисперсию (не факт), во втором — глобально делим на когорты, тем самым экстраполируем эффект на весь трафик. Кейс из практики: мы устанавливаем виджет с такси только на главную страницу нашего сайта и только для пользователей, у кого накопилось более 20 000 баллов. Тогда используем exposed тест, считаем A2C, получаем бОльший эффект, чем при подсчете метрики глобально.
Вот как все происходит в подавляющем большинстве случаев: случайно делите весь новый трафик из новичков на тест и контроль. На основании опыта или теории получаем ожидаемый размер эффекта, и от него считаем выборку. Получив результаты, проверяем их на статистическую значимость. Дополнительно, можно провести АAB-тест, это позволит убедиться, что различия только на уровне поведения пользователей, а не на уровне багов системы, изменения погоды и прочих факторов. Аудиторию перед тестом можно раскидывать простым рандомом, а можно престратификацией (CUPED). Если почти все пользователи новые, то CUPED с дополнительной ковариатой.
В идеальном случае после запуска теста через определенное время тест проверяется, и делается переоценка кол-ва дней, нужных для сбора данных. Торопиться при сборе данных не надо, средний цикл оформления банковской услуги это 2 недели, значит, это минимальный срок для сбора данных. Данные влияют на качество валидации гипотез, обязательно проверяем стабильность данных (отсутствие шума), исходя из исторических данных.
Данные не обязательно собирать самостоятельно, основные источники данных это:
1. Данные из собственных приложений, сайтов, расширений и т.д (CRM, ERP, транзакции, метрика, Amplitude).
2. Снифферинг незашифрованного траффика на крупных узлах обмена данными.
3. Покупка данных сторонних поставщиков — создателей приложений, расширений, рекламных/баннерных сетей, малвари, червей и т.д., как легитимным, так и не очень образом.
4. Открытые данные рынка и исследования агентств (Росстат, GFK).
5. Сырые events из продукта.
6. Покупка данных о посещаемости каких-нибудь ресурсов, которые готовы продать данные.
7. Хантинг людей, опросы и исследования, фокус-группы.
Характеристика и нормализация данных
Предположим, данные готовы, они могут быть в формате csv или Excel. Их может быть много или мало, плотность распределения вероятностей среднего значения выборки может быть нормальной и ненормальной. Проверка на нормальность данных нужна, чтобы центральная предельная теорема выполнялась на малых выборках. Если выборки большие и наблюдения независимые, то предположение о нормальном распределении для теста Стьюдента не нужно (т.к. работает центральная предельная теорема). На 1000 пользователях не удастся отследить мелкие изменения (1-2%), но изменения в 20-30% можно. Проще говоря, при большой выборке результаты теста будут точные, при маленькой выборке не факт, что есть смысл проводить A/B тест.
Предположим, что данных мало, значит, нужна проверка о типе распределения данных. Не факт, что удастся отличить равномерное распределение от нормального на очень маленькой выборке. В общем случае, нужно построить график столбчатой диаграммы и посмотреть его форму. Нормальное распределение выглядит как колокол с тремя сигмами с каждой стороны. Правило трех сигм: каждая сигма это одно стандартное отклонение, данные нормально распределены, и 99,7% выборки попадает влево по графику на три сигмы, и вправо по графику на 3 сигмы. Если выборки гомогенные и распределение нормальное, то наш выбор это t-Критерий Стьюдента. На Стьюденте сложно контролировать мощность, и значит, растет шанс совершить ошибку второго рода. Если же по графику видно, что распределение с отклонением на левую сторону графика, то используется хи-квадрат Пирсона, это непараметрический критерий. Он хорошо подходит для проверки равномерного налива трафика, но требует сгруппировать данные по бакетам (создать таблицу сопряженности). Если распределение отлично от нормального, то правило трех сигм — не лучший выбор, если наше распределение вырожденное. Но на картинке ниже слева распределение вполне может быть логнормальное, и можно отрезать по квантилям.
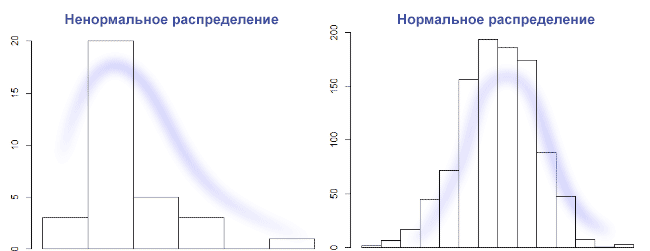
Встречается еще мультимодальное или бимодальное распределение, но чаще после ресемплинга. Если мы говорим про оценку средних, то при достаточном кол-ве наблюдений данные будут распределены нормально. Это большой плюс работы над крупным продуктом, в котором всегда много данных: при любом распределении исходных величин распределение выборочных средних будет стремиться к нормальному. Результат попросту зависит от мощности, т.е. от размера выборки. Идеально нормальных данных быть не может, если под реальной жизнью не понимать результат работы функции rnorm(). Да и данные в нашем случае дискретны и являются набором точек. Поэтому на большой выборке shapiro-wilk всегда будет значимым. А вот на выборках 10-15 значений он всегда незначимый из-за недостаточной мощности. В статистике мощность асимптотически стремится к 1.
Мощность это вероятность допустить ошибку первого рода, то есть отклонить нулевую гипотезу, хотя она верна.
Стратификация (выделение суб-группы из выборки и рандомом деллим на 2 группы) не плохо работает для однородности. Страта это группа наблюдений, подчиняющихся единому правилу. Стратифицированный метод предпочтителем, когда мы сначала делим людей по какому-то признаку (например, по полу), а затем берем людей из этих групп в равной пропорции. Если люди распределяются между двумя группами полностью случайно, то ни о какой статистической значимости речи быть не может.
Сегментация нужна. Хотя бы на уровне киты/планктон и рандомом, сверяясь на A/A-тесте. Или по странам, месяцу регистрации. Если нет параметрического критерия, тогда делим данные на две одинаковые группы, задаем α — уровень значимости, n — размер выборки, mde — эффект. Одну из групп сдвигаем на mde, применяем критерий и бутстрэп.
Итоговый процент принятия нулевых гипотез будет 1 — β. По завершению A/A-теста важно посмотреть на распределения p-value. Оно должно быть равномерным. Если наблюдается скос, то значит, есть сильные зависимости между данными и анализ делать нельзя. А вот для a/b такой подход не пойдёт.
И даже так выборки могут быть с нестабильным по времени и с дисбалансом. Поэтом важно выбрать подходящий критерий для таких выборок. Ресемплинг поможет для оценки, как и моральная подготовка к перезапуску теста при наличии скачков данных на ретроспективе.
Выбросы надо смотреть на box-plot и удалять ручками, как и дубли. Если мы работает с финансовыми метриками и удалять выбросы невозможно, то значит увеличивается разброс значений и доверительные интервалы также увеличиваются. Применяется правило трех сигм: убрать все значения, которые выходят за три стандартных отклонения и посмотреть, как изменятся наши данные. Но будет большая потеря данных, что может быть критично. Другой способ это метод трансформации по Боксу-Коксу. При этом надо понимать, что удаление выбросов только для применения того или иного критерия—не верный подход. Прагматичнее для начала посмотреть срезы, где явно будут видны различия.
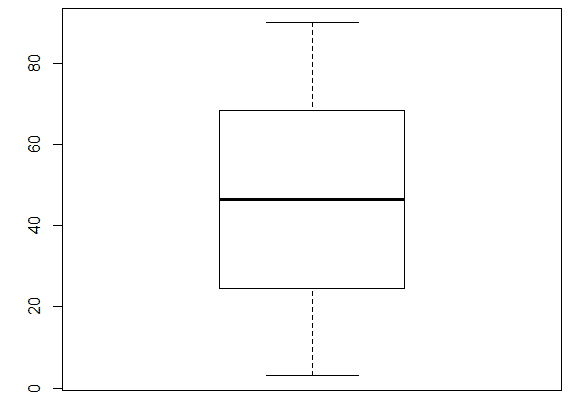
Давайте сгенерируем данные таким способом usersExport <- data.frame(n = 3:90) и построим график boxplot(usersExport). Мы получим практически идеальный график, на котором есть квантили.
Как читать график boxplot: точка или линия соответствуют средней арифметической, эту точку окружает квадрат, его длина соответствует точности оценки генерального параметра. Усы от квадрата соответствуют своей длиной одному из показателей разброса или точности. Для формирования boxplot нужно написать комманду boxplot(имя переменной). Можно для эксперимента создать дырки в данных usersExport <- usersExport[-sample(3:90, 23), ] и посмотреть, как изменится график boxplot.
Вот пример графика с выбросами:
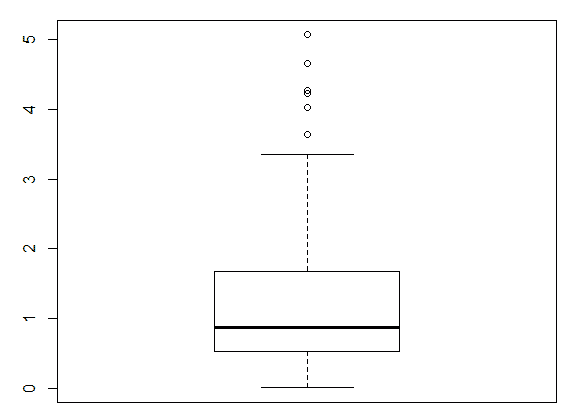
Проверить данные на нормальность можно простым взглядом по qqplot(). При больших объемах тесты практически всегда покажут отклонения от нормального распределения. Поэтому, если данные получились очень ненормальные, например у времени, проведенного за смартфоном или финансовых показателей всегда есть ограничение снизу, то нужна нормализация или хотя бы удаление выбросов. Переходя к цифрам, различие в 5% не такое уж и большое. На большой выборке будет совсем близко к 0,05. Кроме того, многие тесты устойчивы к умеренным отклонениям от нормального распределения. Даже очень небольшие отклонения от нормальности будут значимы на больших выборках, но это справедливо для всех стат. тестов.
qqplot(rt(a,df=3), x, main="t(3) Q-Q Plot") abline(0,1)
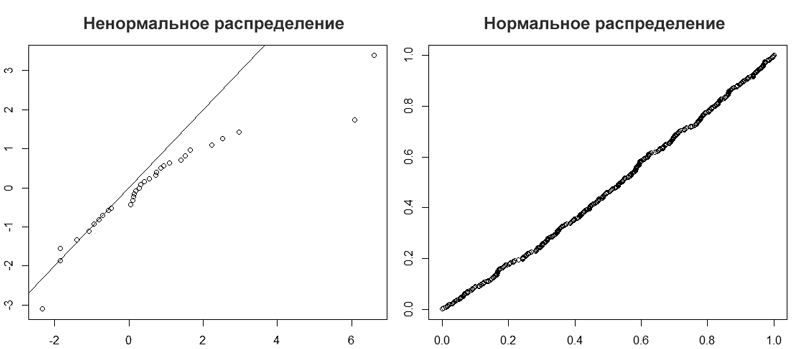
Мы видим, что R-Studio нарисовал график Q-Q (слева). На таком графике отображаются данные в отсортированном порядке по сравнению с квантилями из стандартного нормального распределения. За исключением выбросов, точки расположены более менее по прямой, хотя и скашиваются. Значит, наши данные искажены. На это также указывает, что точки расположены вдоль линии в середине графика, но отгибаются в конце. Такое поведение характеризует наличие в выборке более высокие значений, чем ожидалось от нормального распределения. Пример нормального распределения показан на графике Q-Q справа.
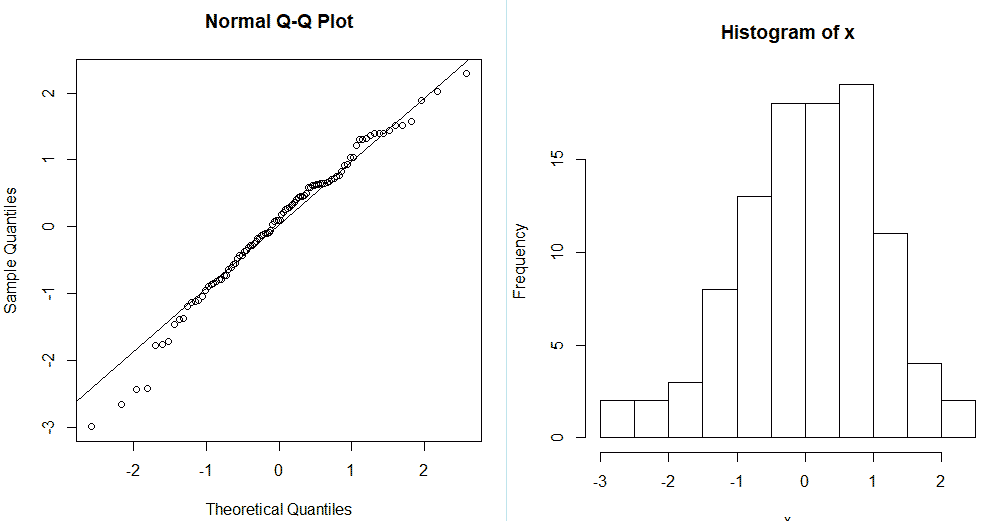
Еще один пример нормальных данных: вводим команду для генерирования данных x <- rnorm(100). Строим график с линией qqline(x), и добивает гистаграммой hist(x).
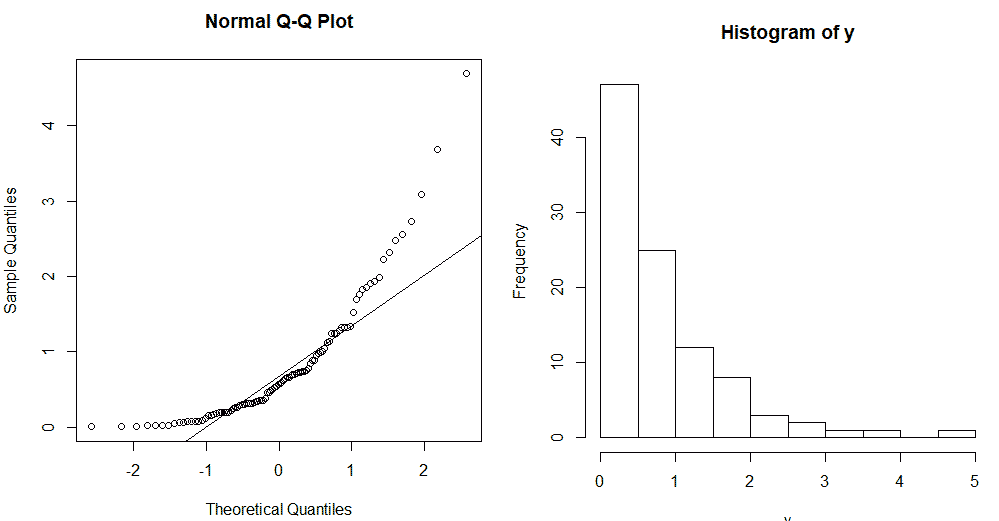
Пример ненормальных данных: y <- rgamma(100, 1), затем qqnorm(y); qqline(y), и гистограмма hist(y).
Выбираем победителя
В зависимости от количества и нормальности данных мы выбираем разные критерии для выявления победителя. Если данные нормально распределены, то используем бернулевский тест, гаусовские расчеты. Смотрим степени свободы, победил вариант, не победил вариант.
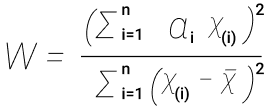
Для начала рассмотрим тест Шапиро-Уилка как критерий для определения нормальности, он очень мощный. Критерий Шапиро-Уилка это W-критерий, который также позволяет оценить нормальность. Если W=1, то выборка точно нормально распределена. Так, нулевая гипотеза = выборка принадлежит нормальному распределению. Если Шапиро-Уилка дает маленький p-value, то значит есть выбросы. Все, что выше 0,75, можно считать нормальным распределением. Для выполнения теста Шапиро-Уилка предназначена функция shapiro.test(x), принимающая на вход выборку x объема не меньше 3 и не больше 5000. Генерируем нормальные данные, x <- rnorm(4600), и используем тест shapiro.test(x). Мы видим следующий текст:
Shapiro-Wilk normality test data: x W = 0.99947, p-value = 0.222
Смотрим на p-value = 0.222 и принимаем нулевую гипотезу.
W это значение статистики теста, в данном случае это 0.99947, что считается отличным результатом, т.к. выборка изначально имеет нормально распределенные данные. Чтобы отклонить нулевую гипотезу, p-value должно быть не выше альфы 0,05 (максимум 0,1). Проверим на ненормальных данных: y <- rgamma(100, 1), shapiro.test(y).
Shapiro-Wilk normality test data: y W = 0.9829, p-value < 2.2e-16
P-value < 2.2e-16, что намного меньше 0.05, практически 0. И это при том, что R сообщает только значения p-value выше порога 2.2×10−16. Мы отклоняем нулевую гипотезу. Сначала смотрим, меньше ли 0.05, потом сравниваем средние или медианы. На несимметричных данных медиана значительно лучше отразит центральную тенденцию, чем обычное среднее. Если распределение одной из выборок заметно отличается от нормального, то в качестве центра берется медиана и соответственно, критерий Уилкоксона — Манна-Уитни, непараметрический и хорошая замена Хи-квадрату Пирсона. Если у данных положительный длинный хвост (прибыль) и ненормальное распределение, то это Манна-Уитни, перестановочные тесты или бутстреп. Перестановочные тесты про гипотезу о схожести распределений двух выборок.
Если же распределение всех выборок нормальное, то среднее арифметическое это наш выбор, и какой-либо из Стьюдентов (критерий сдвига).
Проблема это ограничение на 5000 наблюдений. Если наша выборка больше, то применяем Shapiro-francia w’ test. Или Anderson-Darling test, его попроще найти в готовом виде, он может проверить данные на любые распределения. Либо тест Колмогорова-Смирнова (критерий согласия), но для решения реальных задач лучше его не использовать.
A/B-тесты подразумевают два набора данных, поэтому тест нужно проводить для обоих выборок. Это не обязательно тест Шапиро-Уилка, это может быть и непараметрический ранговый U-критерий Уилкоксона — Манна-Уитни. Проверяет гипотезу сдвига, кушает любые выборки, но понятное дело, что обе выборки должны быть примерно схожи по распределению. Тест робастый, оперирует рангами. Сдвиг это не про проверку медианы, а про проверку «скошенности» данных относительно друг друга. Если в одной выборке у нас значения [2,3,4,5], а во второй [5,6,7,8], то это явно сдвиг.
Если данные непрерывные, то в простых случаях хорошо работают критерии Уилкоксона — Манна-Уитни/Краскела-Уоллиса, в которых нулевые гипотезы на сравнения распределений и медианы. Распределение 50 на 50 подразумевает использование формулы Бернулли, а может быть и Байесовский многорукий бандит. Если же использовалось сплит-тестирование, то нужно использовать непараметрический дисперсионный анализ — критерий Краскела-Уоллиса. Для сравнения дисперсий хороший вариант Fligner-Killeen и Brown–Forsythe. Рассмотрим с примерами.
Подход Байеса рекомендуется при большом количестве данных, альтернатива частотному подходу. Частотный подход про нулевую гипотезу и про частоту событий, Байес — про принятие нулевой гипотезы, позволяет работать с событиями и причинами. Нельзя применять Байеса и частотный подходы одновременно, это ведёт к «парадоксу Линди».
Частотный подход не позволяет сделать предположение заранее, предлагается полагаться на данные тестовой выборки. Мы повторяем эксперимент бесконечное количество раз для получения гистограммы объективной неопределенности. Сама гипотеза проверяется по классическому p-value. Важно зафиксировать размер выборки до эксперимента, вот две формулы для этого: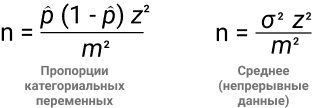
- В числителе находим дисперсию (α2), в знаменателе mde.
- z — стандартная ошибка, 1,96 при 95% уровне значимости.
- σ — стандартное отклонение.
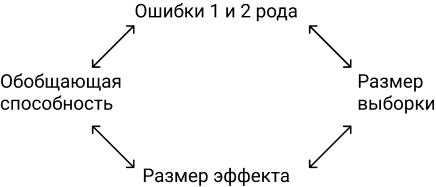
Обратите внимание, что практически все переменные взаимосвязаны. Чем меньше эффект, который мы хотим поймать, тем больше размер выборки.
Обобщающая способность. Если мы возьмем гомогенную выборку, то дисперсия будет меньше, функция плотности вероятности будет более сконцентрированная, чем при 100% доступных данных. Но и выводы по гомогенной выборке будутрелевантны выборке, а не всем данным. Вывод: меньше дисперсия = меньше обобщающая способность.
Давайте на примере. Нужно найти размер выборки для теста пропорции категориальных данных. α = 95%, mde = 0.05, p = 70%, z = 1.96. Так, n = 1.96^2 * 0.7 * (1 — 0.7) / 0.05^2 = 3.8416 * 0.7 * 0.3 / 0.0025 = 322.
Идея Байеса в получении 500 раз выпадение орла из 1000 бросаний монетки, и считается по формуле C500(1000) * 0.5^(500) * 0.5^(500), т.к. броски друг от друга никак не зависят. Если бы мы знали все возможные параметры монетки, мы могли бы предсказать результат. Но так как это невозможно, то проводим множество наблюдений. Байес позволяет ответить на задачу индукции, какой из вариантов лучше и на сколько. У Байаса всегда есть априорное распределение, а значит, нужно иметь свои представления о параметрах исследуемового процесса. Что, в принципе, является основой образа мышления дизайнера. Для Байеса можно не считать мощность и значимость, но пропадает понимание эффекта. Если по каким то причинам не нравится Байеc, то можно использовать Стьюдента или Бернулли для больших выборок. Если результаты 0 и 1, то точно Бернулли и биномиальное распределение. А с ним легко работать, интерпретировать, визуализировать.
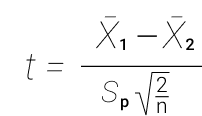
Стьюдент. T-тест или определение t-критерия Стьюдента является простейшим способом проверки точности среднего значения для данных с естественными значениями. Выборки должны быть независимыми (не парными) и нормально распределенными (чем больше результатов, тем ближе распределение к нормальному). Это гарантирует концентрацию плотности значений вокруг среднего значения, что позволяет делать выводы о генеральной совокупности, имея только информацию о выборке. Провести тест легко: x = rnorm(1000000) и y = rnorm(1000000). Команда t.test(x,y). Получаем следующие данные:
data: x and y t = -1.1696, df = 2e+06, p-value = 0.2422 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.004424298 0.001117388 sample estimates: mean of x mean of y -0.0007571144 0.0008963404
И проверяем:
m = length(x); n = length(y) t = ( mean(x) - mean(y) ) / sqrt( var(x)/m + var(y)/n ); t
В обоих случаях получаем t = -1.1696, и p-value = 0.2422. Так как мы всегда обеспокоены тем, является ли p больше или меньше 0,05, то при 0.2422 > 0.05 есть основания не отвергать нулевую гипотезу. P-Value это достигнутый уровень значимости (пи-величина)—наименьшая величина уровня значимости, при которой нулевая гипотеза отвергается для данного значения статистики. По P-Value происходит проверки (и отклонения) «нулевой гипотезы». Чем меньше значение Р, найденное для набора результатов, тем меньше вероятность того, что результаты случайны. Результаты считаются «статистически значимыми», когда это значение ниже 0,05 (или 5%). Если удастся довести значение до 0,005, то уже хорошо, сильно уменьшится количество позитивных неправильных результатов. При 0,05 считается нормой 1/3 неправильных выводов. В идеальном мире даже 0,005 должно быть лишь приблизительной наводкой на финальное решение. В физике или при исследовании генов используется 0.0000003. Чем ниже значение p, тем выше перевес в пользу альтернативной гипотезы.
В примере ниже я визуализировал, как границы меняются в зависимости от входных данных, и в момент выхода за границы принимаем H1 о наличие различий. Различия могут быть на уровне среднего значения, медианы, и не только. Не обязательно делать динамические границы, можно и статичные.
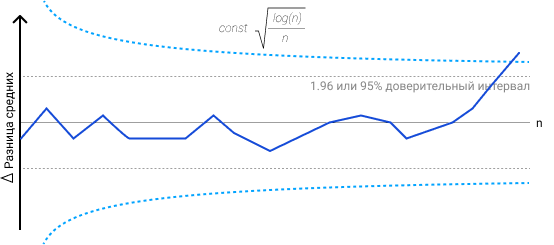
Нулевая гипотеза всегда про отсутствие статистической значимости в результатах, т.е. о равенстве значения генеральной совокупности относительно выбранного критерия. Она зовется нулевой, так как отрицание это ноль, а согласие это единица. Например, все пользователи видят баннер. Альтернативная гипотеза скажет, что не все пользователи видят баннер, т.е. нет утверждения о равенстве параметра генеральной совокупности заранее заданному значению.
Парный t-тест имеет уменьшенное количество степеней свободы, но при этом устраняется влияние индивидуальных различий. Нужен для сравнения зависимых выборок, он мощнее непарного t-теста. Зависимые выборки это когда элемент из контрольной группы имеет соответствующий ему элемент во второй группе. Например, при тесте одинаковой главной страницы в сентябре 2018 года и в сентябре 2019, или навыки дизайнеров до и после курсов. при зависимых выборках нас интересует, как изменения в одной группе повлияют на другую.
leftGroup <- c(12, 13, 11, 15, 19, 15, 17) rightGroup <- c(14, 14, 16, 16, 18, 14, 15) t.test(leftGroup, rightGroup, var.equal=TRUE) t.test(leftGroup, rightGroup, paired=TRUE)
Получаем p-value = 0.5648 в первом случае и p-value = 0.4539 во втором. Очевидно, что дискриминационная способность у парного теста больше.
Второй по популярности — z-тест пропорций. Это параметрический тест, проверяет равенство средних. Видим биномиальное распределение, применяем z-тест. Например, для метрик отношения/конверсии. Тестируется биномиальная случайная величина (орел или решка, 1 или 0, Да или Нет), значит, z-тест. Нужна независимость выборок. Если же задача в сравнении равенства дисперсий, то наш выбор это Levene, тест Бартлетта. Они параметрические, тест Бартлетта будет помощнее, но и требует более нормальное распределение, чем Levene.
Следующий критерий, Уилкоксона — Манна-Уитни, позволяет протестировать, что результаты случайных наблюдений из одной группы могут быть выше, чем в другой. Это непараметрический критерий, альтернатива t-test. Идея такая: для t-test нужны нормально распределенные данные (нормальность среднего распределения) и его результаты легко интерпретировать, но он чувствителен к выбросам. Если у нас нет информации о нормальности распределения, используем критерий Манна-Уитни, имея ввиду, что он не покажет тонких различий между выборками и его сложнее интерпретировать. Причина в том, что t-критерий работает на основе сравнения средних из фактических наблюдений, в то время как критерий Манна-Уитни использует сравнение рангов (номеров наблюдения в упорядоченной выборке), что позволяет ему быть устойчивым к выбросам. Но при этом критерий Манна-Уитни весьма чувствителен к различию дисперсий, и на больших выборках это становится очень заметно.
Поэтому на практике допускается использовать t-test для оценки средних на большой выборке, так как нормальность обеспечивается «сжиманием» крайних значений по ЦПД (чем больше элементов в выборке, тем меньше дисперсия среднего арифметического). Но при этом помним, что чем больше отклонения от нормальности, тем хуже тест сравнивает выборки. Так что t-test не подойдет для небольших выборок из ненормального распределения, но подойдет для большой выборки из ненормального распределения.
T-test чувствителен к выбросам, и если есть длинный хвост в данных (а он почти всегда есть на реальных финансовых данных), то такой хвост сильно скажется на среднем, и за счет большой дисперсии получим плохой результат работы критерия. Любые популярные метрики, вроде ARPU, количество сессий, время чего-либо, ARPPU, средний чек это не биномиальное распределения. И зачастую они не поддаются анализу параметрическими тестами, длинные хвосты и значит, большее количество денег мы получаем от небольшого кол-ва пользователей. Это можно решить за счет техники бакетов, но опять же, нужна большая выборка. Если маленькая выборка, тогда у нас выбор: либо U-критерий Манна-Уитни, считаем p-value внутри дней с поправкой на множественное сравнение, теряя в мощности. Если можно избежать применения поправок — лучше избежать. Либо накопительный p-value. Либо bootstrap как самое простое решение, получим распределение выборочного среднего и посмотрим на пересечение квантилей с заданным уровнем значимости. Либо CUPED преобразует данные в нормальные, уменьшив отклонения от среднего, и T-Test с поправкой Уэлча. Либо mood’s median test, но понадобится таблица сопряженности.
Используем команду wilcox.test(mpg ~ am, data=mtcars) получаем сообщение, “не могу подсчитать точное p-значение при наличии повторяющихся наблюдений”. Если вас смущает это сообщение, измените команду на wilcox.test(mpg ~ am, data=mtcars, exact=FALSE). Это объяснит программе, что мы все понимаем, и не ждем точного расчета p-value. Получилось W = 42, p-value = 0.001871. Напомню, P-Value должно быть не выше 0,05.
А теперь возьмем два набора наблюдений и протестируем:
a = c(123, 105, 147, 142, 119, 129, 130, 87 ,301, 92, 177, 141, 137, 112, 138, 128, 114, 197, 198, 210, 101, 125, 134, 214, 110, 100, 152, 122, 144, 148 ,153 ,212) b = c(154, 512, 120 ,131 ,124 ,118 ,178 ,140 ,136, 68, 162, 127, 78 ,106, 133, 655 ,155 ,169 ,199 ,108 ,143, 341 ,121 ,139, 166, 174, 184, 98, 135, 132, 146, 209)
wilcox.test(a,b)На выходе получаем:
data: a and b W = 455, p-value = 0.4507 alternative hypothesis: true location shift is not equal to 0
У нас есть наше любимое P-Value, которое куда больше, чем 0,05. Мы принимаем нулевую гипотезу. W является статистической статистикой Уилкоксона и, как следует из названия, является суммой рангов в одной из двух групп.
Если р < 0,05, то нулевая гипотеза про отсутствие отличий отвергается.
С Бернулли схожая история, берет два вида данных (орел/решка, мальчик/девочка, красное/черное). rbinom(200, size = 1, p = 0.68) где p это шанс получить 1. Грубо говоря, rbinom скажет, сколько будет орлов, если сыграть определенное кол-во раз в монетку. Пример показывает сразу 200 испытаний Бернулли. Посмотрим, как мы можем сравнить два испытания Бернулли, т.к. данные очень похоже на результат бинарного A/B теста:
varA <- rbinom(200, 20, 0.5)
varB <- rbinom(200, 20, 0.25)
И используем hist(varB, probability = TRUE, col = gray(0.9)) для двух наборов данных. На графиках мы видим 200 биномиально распределенных случайных чисел для испытаний размером = 20 и с разной вероятностью возникновения интересующего нас события p = 0,25 и 0,50.
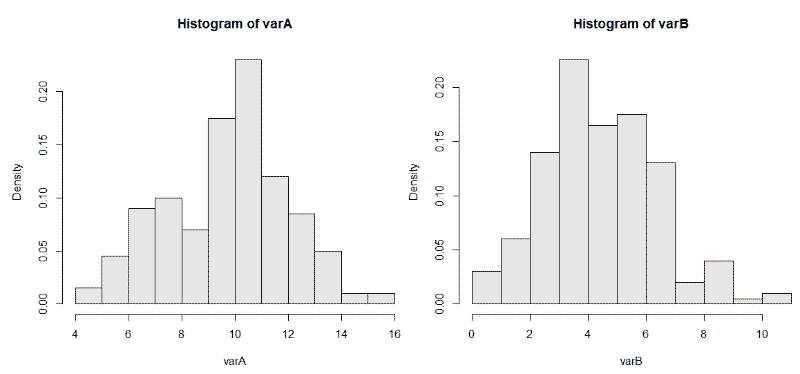
Биномиальные критерии это сравнение пропорций. Позволяют проверить гипотезу про коэффициент удаления приложения. Если выборка маленькая (100), конверсия в покупку 12%, то биномиальный тест лучший выбор. Стьюдент может быть применен к распределению Бернулли, но выборка маловата, должно быть > 200. В данном примере, с бутстрепом будет аналогичная история.
Говоря о типичных финансовых данных, где есть пик-скопление небольших платежей + длинный хвост, и нас не пугает работать с логарифмом от некой велечины (но не от 0), то методом Бокса-Кокса можно транформировать данные в нормально распределенные. Простой логарифм от числа, который тем не менее усложняет интерпретацию результатов. После этого берем привычный параметрический тест (t-критерий Стьюдента), смотрим p-value и оцениваем уровень значимости для закрытия эксперимента.
Процесс выглядит так: узнаем про выбросы с помощью boxplot, проверяем выборку на нормальность с помощью теста Шапиро Уилко, охарактеризовать распределение с помощью QQnorm, и выбрать метод анализа. Если данные нормальные, используем Бернулли, Гаусса, Стьюдента. Ненормальные (график сглажен по одной из сторон): Хи-квадрат, Байес, Пуассон. Обычно данные выглядят как диапазон от 0 до десятков в кучей выбросов до нескольких сотен, и это распределение Пуассона. Распределение Пуассона применяется в теории массового обслуживания. После этого оцениваем параметры, учитываем их при запуске теста хи-квадрат к выборке и распределению Пуассона, и получаем ответ про правильность гипотезы при распределение Пуассона.
Итак, тест прошёл. На что мы можем посмотреть? В первую очередь, нельзя подгонять новые гипотезы по факту завершения эксперимента под найденную разницу, хотя очень хочется. Называется это P-hacking, когда сначала идет сбор данных, проверяют множество разных гипотез, и те, которые соответствуют p<0.05, публикуют в научных журналах. Если вы работаете в науке и нужно собирать гранты на новые научные изыскания, то все на вашей совести. Но в бизнесе такой подход недопустим.
Могло показаться, что t-test это участь исключительно научной работы и он не применим для бизнес-задач. Но вот пример: возьмем метрику отношения (ratio metric), например CTR. Посчитаем соотношение суммы кликов и суммы просмотров, их отношение это конверсия в клик. В таком примере данные зависимы и не можем использовать t-test.
Другой тип метрик это поюзерная метрика. Смотрим на среднее значение, т.е. был ли открыт лутбокс, или нет. Здесь у нас одинаково распределенные, независимые случайные величины, и мы можем применить t-test. А теперь магия: мы можем использовать линеризацию для превращения метрик отношения в поюзерные метрики. При этом не теряется чувствительность и метрика сонаправлена с изначальной.
После теста проверяем, все ли пользователи завершили целевое действие. Например, среднее время жизни пользователя сервиса для генерации временных e-mail адресов составляет 5 дней. В выборке не должно быть тех, кто начал пользоваться сервисом за 5 дней до конца эксперимента.
Нельзя допускать аномальных всплесков в ходе эксперимента, они могут внести статистически значимый вклад в результат.
Если у нас биномиальная метрика, то надо смотреть на изменение мощности. Например, обе наблюдаемые группы резко скатились вниз, и это сказывается на мощности. Ближе к концу эксперимента можно пересчитать и сделать вывод, сильно ли отличается мощность в конце и начале эксперимента. Сильно отличается в худшую сторону? Продолжаем эксперимент, ждём нужную мощность.
P-value тоже имеет свой доверительный интервал. Если провести 10000 A/A-тестов при p-value=0.05, то мы ожидаем, что 500 прокрасится. Даже у этих 500 есть доверительный интервал, некий доверительный интервал доверительного интервала. Помогает вероятностный подход: классическая теорема Байеса.
Не только R
Сейчас любой аналитик (не важно, UX, бизнес, дашбордист, ресерчер, разработчик) должен уметь в R и Python. Но базовый навык работы в Excel по прежнему помогает быстро решать многие задачи. При работе над продуктом требуются быстрые выводы по популярным метрикам, dau/mau, конверсия в регистрацию, и показатели метрик часто меняются. Распространенная практика это использовать среднее для всех первичных KPI, если распределение нормальное. Это позволяет делать первичные выводы очень быстро. Понять тип распределение можно с помощью стандартного/среднеквадратичного отклонения. в Excel для этого используется функция =сроткл. Формула выглядит как STD=√[(∑(x-x)2)/n], и расшифровывается как корень из суммы квадратов разниц между элементами выборки и средним, деленной на количество элементов в выборке.
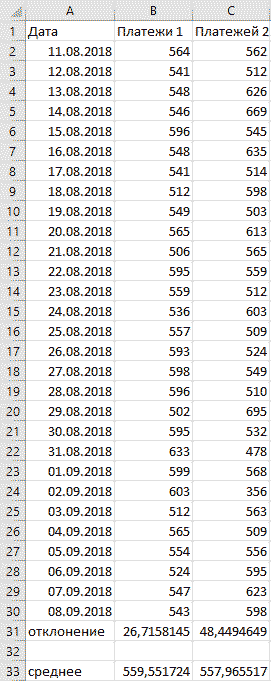
В примере выше видно, что, не смотря на практически одинаковые средние значения, видны огромные колебания данных вокруг среднего значения второго варианта. Первый вариант заслуживает больше доверия.
В Excel еще много замечательных способов визуализировать данные, особенно полезны сводные таблицы. Работают по принципу вирутальной группировки строчек с одинаковыми названиями товаров. Берется группа и считается для нее сумма, очень удобно. Такие таблицы используются для агрегирования данных и получения отчета.
Главное при проведении тестов это умение делать выводы из цифр, критически мыслить, делать выводы на основе исторических данных, генерировать гипотезы, рассуждать, чувство рациональности и нерациональности. Математический анализ лишь помогает не принять вымысел за правду, но окончательное бизнес-решение принимает по прежнему специалист.

45 комментариев
Andrei Ivashkevich
Здравствуйте, спасибо за статью. Есть ли способ легко уместить датасет в определенный диапазон?
Цветков Максим
На примерах: создадим данные
Смотрим на гистаграмму,
hist(x), данные не очень то нормальные. В данном искуственном случае требуется предварительно сделать логарифмирование. Это самое простое преобразование, очень помогает. Сильно бьет по большим отклонениям, после логарифма данные ужимаются и выбросы приближаются к основной части распределения. Либо сразу использовать непараметрику. Или обрезать выбросы, но с пониманием проблематики: в играх выбросы или читеры, им надо уделять особое внимание. На продуктовых метриках построить три сигмы и остальное вырезать — точно не вариант, так как аномальное поведение ≠ нет ценности для бизнеса. При этом нужно понимать, что выбор способа трансформация зависит от типа данных и направления асимметрии.Можно усложнить себе задачу:
Проверим
plot(density(x)), данные сместились, теперь нормализация по Боксу-Коксу не сработает.Пару раз встречал решение вида g <- runif(x), не надо так делать, это генерация случайных данных. А вот что-нибудь вроде
уже ближе к истине. Принцип: значение минус среднее значение и разделить на стандартное отклонение переменной. Результат будет иметь среднее value = 0 и sd = 1. Строим график
qqnorm(finalData). Это стандартизация данных, т.к. преобразование данных, поэтому стандартное отклонение 1.Можно просто привести все цифры к диапазону от 0 до 1, возможно, вы это и имели ввиду.
Также, распространенный способ это
x[!x %in% boxplot.stats(x)$out], который также не меняет данные, но фильтрует.Даня
Здравствуйте. Есть ли варианты выгрузить данные из GA напрямую, без CSV?
Цветков Максим
Сначала нужно установить правильные библиотеки,
install.packages("RGA")иinstall.packages("devtools"). И подключитьlibrary(devtools),library(RGA). Даем доступ к данным в GAauthorize(username = "ваш gmail"), вас перебросит в браузер и будет сформирован код, который нужно будет вставить в R. Будет создано окружение .RGAEnv, которое не видно пользователям.В скриптах часто нужно прописывать проверку существования объекта:
x <- NAи затем
exists("x").list_profiles()позволит определить идентификатор профиля, с которым вы планируете работать. И можно потестировать работу командойget_ga(), сделав запрос данных у Core Reporting API, и получить информацию вида users 333/sessions 486/pageviews 1505 по первому найденному profileId. Подробный хелп будет по командеbrowseVignettes(package = "RGA").И финальная команда,
Запросы можно формировать сколько угодно сложные, т.к. API очень хорошее.
Работать с регулярными выражениями
При работе с регулярными выражениями можно использовать следующие операторы:
= — точное соответствие;!= — отсутствие равенства;
=@ — содержит подстроку;
!@ — не содержит подстроку;
=~ — соответствует регулярному выражению;
!~ — не соответствует регулярному выражению.
И потом это все легко визуализируется
Можно строить сложные графики:
Артём Клевцов
Спасибо, я пытался по одной статье делать, не получалось, ваш пример сработал. Буду разбираться дальше. Мне выпало очень много результатов not provided, что это такое?
Цветков Максим
Большое количество not provided встречается при большом количестве органического трафика. т.к. речь только об органическом трафике, проплаченный трафик Adwords будет показывать слова в PPC.
Можно с помощью фильтра извлечь все «not provided», это поможет понять, откуда шел трафик.
Еще можно настроить фильтры таким образом, чтобы было видно, на какие страницы приходят пользователи из not provided.
В Google Search Console также много ключевых слов, и в нее можно дозагрузить слова из метрики.
Денис Ильин
Есть ли способ красиво выстроить по возрастающей диапазон дат?
Цветков Максим
Не уверен, что понимаю контекст вопроса. Первое, что приходит на ум:
А как украсить, тут довольно субъективный вопрос, что такое красиво. Попробуйте использовать библиотеку для красивых цветов:
После того, как выберите подходящие вам цвета, используйте следующую команду. Я добавил немного случайности порядку данных:
Max Proskin
Для использования Фишера и Хиквадрата на матрицу данных из двух наблюдений требуется много или мало данных? Если данные из опросника и содержат данные для метрик типа SUS SUM. И как лучше визуализировать такого рода данные?
Цветков Максим
Сгенерируем матрицу распределения двумерных данных:
matrixData = matrix(1:9,800,2). Функция берет вектор и преобразовывает в матрицу с колонками. Предположу, что наблюдения являются независимыми и мы можем смело использовать Хи-квадрат или Фишера. Числа обязаны быть абсолютными и качественными. Возьмем Хи-квадрат для проверки нормальности распределения данныхchisq.test(matrixData). RStudio предупредит о возможной некорректности результатов, потому что хи-квадрат плохо работает, если числа небольшие.Возьмем другую матрицу данных:
matrixData = matrix(1:5,6,2). Запускаем тест Фишера:fisher.test(matrixData). Фишер это F-тест для сравнения дисперсий двух и более генеральных нормально распределенных небольших по объему данных. Не содержит правила, что p-value должно быть фиксированным значением для принятия нулевой гипотезы. Или критерий хи-квадрат Пирсона с коррекцией непрерывности Йейтсаchisq.test(matrixData, simulate.p.value = TRUE). Симуляции нужны для нахождения P-value, позволяет не полагаться на приближение хи-квадрата к распределению тестовой статистики, и искать p-value точнее за счёт применения генератора случайных чисел. Видно, что полученный P-value 0.6436 намного больше, чем 0.05, значит, выборка не противоречит нулевой гипотезе.Если же нужно сравнить медианы, в статистике существует критерий для медиан Муда, который не очень популярен на рынке из-за большой ошибки второго рода. Но все же пример приведу. Допустим, есть две выборки по использованию продукта в Cеверной и Западной Европах. Из коробки теста Муда в R-Studio нет, но его можно симулировать следующим образом:
В приведенном примере P-value = 0.01225, который меньше чем альфа 0.05 (ошибка первого рода), гипотеза о равенстве медиан отвергнута. Значит, использование продукта отличается. Но лучше проверить такие данные критерием Уилкоксона — Манна-Уитни. Он не проверяет разность медиан и работает только с рангами, но проверяет вероятность как часто
X < или > Y. При использованииwilcox.test(x1, x2,alternative="two.sided", exact=TRUE, correct=FALSE)получаем p-value = 0.0007761, который намного меньше альфы.Основная проблема в том, что нельзя доверять такому малому кол-ву данных. Выводы можно делать, только если в каждой колонке сотни или тысячи наблюдений.
Для визуализации подойдут коррелограммы/хитмапы.
Можно получить очень красивые графики:
Виктор
Не могу настроить прокси на Mac под R, что ни делал постоянно вываливаются ошибки с недоступностью серверов. Вручную тоже не получается устаноить пакеты. Можете посоветовать что нибудь?
Цветков Максим
Заходите в Chrome по адресу
chrome://net-internals/#proxy, видите ссылкуscript:http://wpad/wpad.dat, открываете и видите свой прокси.В терминале для включения прокси:
export http_proxy=http://address.ru:8080export HTTP_PROXY=http://address.ru:8080
Можно с именем и паролем:
export http_proxy='http://username:password@address.ru:port/'Отключить можно командой:
export http_proxy=''Не будет лишним проверить в System Preferences → Network → LAN → Advanced → Proxies → включена ли галочка Auto Proxy Detection. Command Line не используют эти настройки, но для другого софта пригодится.
Далее в RStudio:
Sys.setenv(http_proxy="http://address.ru:8080")Для удаления созданного окружения в R:
Sys.unsetenvПроверить, что мы насоздавали:
Sys.getenv("http_proxy")Еще одно решение это установить cntml:
brew install cntlm.Полезно глянуть свой прокси
netsh winhttp show proxy.Evnegy Shel
Если у меня есть набор данных, в каком момент я смогу понять, что мои данные нормально распределены, и как отличить от равномерного распределения.
Цветков Максим
Простой Shapiro-Wilks-W-Test, самый популярный способ, даже популярнее Хи-квадрата:
Получаем W = 0.99518, p-value = 0.1758. P-value больше чем 0.05 говорит нам, что у нас нормально распределенные данные. Если бы p-value было меньше 0.05, мы бы отвергли нулевую гипотезу. Как и
hist(x)в виде колокола. При UX-анализе принято брать уровень значимости 0.05 как вероятность ошибки первого рода. Если 0.49 и меньше, то различия значимы. Это все характеризует нормальное распределение. Визуально оно очень похоже на T-распределение, которое имеет дополнительный параметрdfдля степеней свободы (кол-во значений в распределении, свободных для изменения). Если число степеней свободны низкое, то мы получаем слишком высокие/низкие значения. Пограничное значение это df ≈ 30, при котором распределение становится похожим на нормальное.На полученном графике видно, что синяя линия (нормальное распределение) и красная линия (t-распределение с df=32) очень схожи по форме.
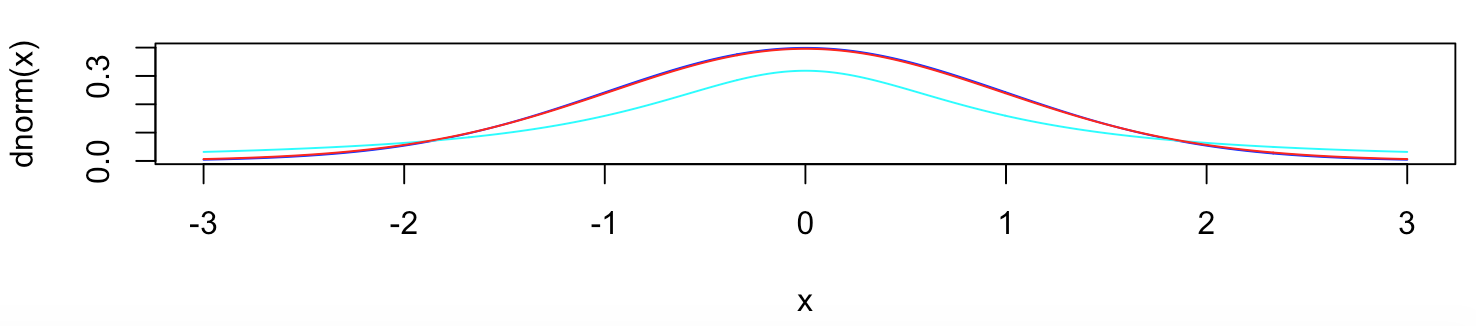
Равномерно распределенные данные можно сгенерировать и сравнить с помощью
runif, в котором r обозначает случайное, а unif равномерное.Или даже гистограммы, для наглядности:
Скорее всего, реальные данные не будут лежать в диапазоне от 0 до 1, поэтому потребуется нормализация (в примере диапазон значений от 15 до 100):
Все вспомогательные значения легко считаются в R:
sd(y)стандартное отклонениеrange(y)диапазон (разница между максимум и минимумом)IQR(y)межквартильный размах (когда есть выбросы)quantile(y, c(0.25, 0.75))квантилиmad(y)абсолютное медианное отклонениеИ всегда есть старый прагматичный подход: проверить и гипотезу о равенстве математических ожиданий, и гипотезу о равенстве медиан, и если ответы совпадут, то выборки одинаковые.
Отдельно скажу про удаление выбросов: на реальных задачах просто взять и удалить выбросы из набора данных нельзя, особенно в eCommerce. Допускается только убрать те наблюдения, которые оказались за 3 стандартных отклонения от среднего, и только если допускается лишиться кучи данных с китами. Еще можно получить логарифм после преобразования с помощью Бокса-Кокса, но тогда мы получим неестественную метрику. Поэтому используем bootstrap, получаем два распределения и на основе квартильной разницы делаем сравнение.
Alexey Sarapulov
Спасибо за команды для получения данных! а есть такие же для вывода самого малого и самого большого значения?
Цветков Максим
Давайте создадим какой-нибудь набор данных:
И выполним команду
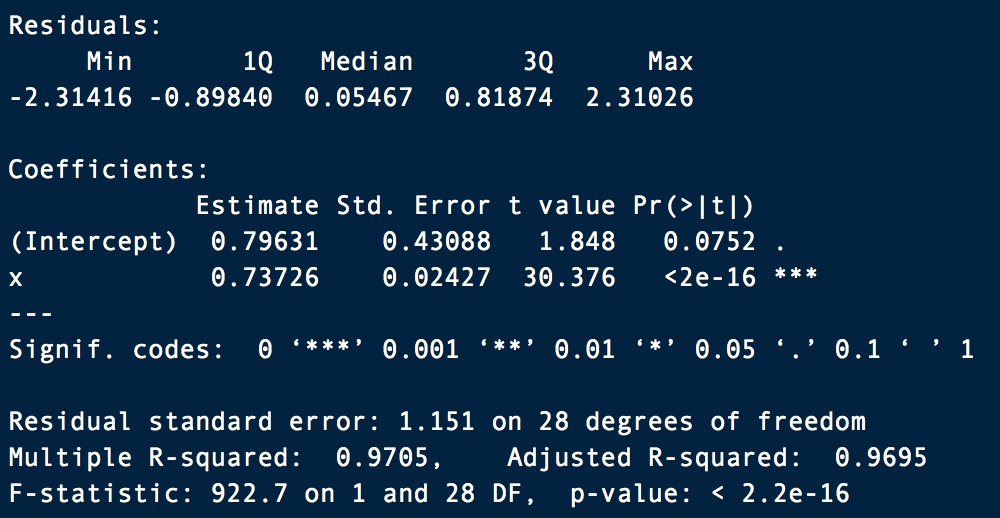
summary(ourData). В результате получим min, max, mean, median, квантили, стандартные ошибки параметров и уровней значимости:Александр Верен
Спасибо, а какой диаграммой вот также сравнить много боксплотов с плотностью вероятностей?
Цветков Максим
Я так понял, вам нужно понять, где больше значений: вокруг медианы или данные сгруппированы вокруг минимума и максимума, а в середине ничего нет. Хорошей альтернативой box-plot служит violin plot, отличаются они тем, что violin plot дополнительно показывает плотность вероятности распределения данных.
Виктор Микронов
Если данные распределены ненормально, но результат выдать нужно, то что делать?
Цветков Максим
Первое это подумать о трансформации данных через Box–Cox, но это рискованная история. Либо работать непараметрическими критериями на основе рангов: W-критерий Вилкоксона или U-критерий Манна-Уитни). В R за оба отвечает
wilcox.testдля двух выборок и тест Крускала-Уоллисаkruskal.testдля большего кол-ва выборок (дисперсионный анализ).Если при верной нулевой гипотезе вероятность получить высокое значение Н-критерия крайней мала, можно эту гипотезу отклонять. Тест Краскела-Уоллиса, как любой дисперсионный, выдет результат вида р < 0.05 (группы различаются) или р > 0.05 (различий нет), не говоря нам ничего о том, в каких именно группах есть различия.
Давайте создадим какую-нибудь матрицу:
Вилкоксон сравнивает не сами значения, а их ранкинг. Получаем
V = 720600, и вероятность случайно получить такое значение при условии, что нулевая гипотеза верна, не больше 0.05 (p-value = 2.2e-16, а это наименьшее число больше нуля, 2.2e-16 < 0.05). Отклоняем нулевую гипотезу. Ремарка: статистические методы, основанные на рангах, не очень хорошо подсчитывают точные p-value при наличии одинаковых значений в данных. Чуть получше с этим у wilcox_test() из пакета coin, за счет аппроксимации распределения критерия Уилкоксона нормальным распределением.Последней строкой мы вернули z-value из результатов Манна-Уитни.
Если нужно сравнить именно средние при ненормальном распределении, то при большом кол-ве данных (больше хотя бы 400 наблюдений) можно и t-критерий Стьюдента, так как в силу центральной предельной теоремы будет примерно нормальное распределение. Либо попросту сравнивать медианы.
В общем, процесс такой:
Данные независимы и A/B, тогда Манна-Уитни. A/B/C+ = тест Краскела — Уоллиса. Это про сдвиг.
Данные зависимы и A/B, тогда тест Уилкоксона. A/B/C+ = тест Фридмана.
Если данные в таблице сопряженности и мы можем сформулировать нулевую гипотезу, тогда хи-квадрат Пирсона.
Ничего не понимаем? Bootstrap, он даст распределение.
Нормальное распределение и A/B, тогда Стьюдент или Welch’s t-test. A/B/C+ = ANOVA.
Разница в дисперсии при нормальном распределении: Бартлетт, Левен, Коновер, по степени удаления от нормальности распределения.
Биномиальные данные: тест пропорций
Anatoly Malanii
Как делается графический способ проверки гипотез A/B теста?
Цветков Максим
Предположим, что данные нормально распределены и среднее является адекватной мерой центральной тенденции. Тогда возникает вопрос, а как можно сравнить два показателя: только подсчитать разницу между ними.
Если вы провели мультивариативный A/B тест, то для каждого варианта надо посчитать CTR и построить графики. График: 95% доверительный интервал для разности средних и медиан (можно бутстрапом), и смотреть, захватывает ли он 0.
Подсчет CTR: у нас 84 343 показов, 21 384 переходов, значит 21 384 / 84 343 = 25.3%.
Андрей
Есть ли способ протестировать разность между двумя значениями медианы?
Цветков Максим
Да, с помощью t-критерия. Это однонаправленный:
А вот двунаправленный:
В результате две выборки значительно различаются (р < 0,05). Следует отметить, что в R не «нормальный» t-критерий, а критерий Уэлча, для которого не важно, чтобы дисперсии обоих выборок были одинаковые (t-test важно). Поэтому может подойти F-тест на идентичность обеих дисперсий:
А дальше все просто, если p < 0,05, то данные в двух выборках значительно отличаются, поэтому необходимо использовать критерий Уэлча, который я привел выше. Но если p > 0,05, тогда дисперсии примерно равны (но не факт), и может быть применен t-критерий:
Если понадобится уменьшить дисперсию, то используйте стратификацию (дробление пользователей на группы, кластеризация для выделения кластеров), использование низкоуровневых метрик (урезание концов), исторических данных (CUPED от Microsoft).
Самюэль Виктор
Я все же не совсем понимаю, вот у вас в статье тест Шапиро Уилка, у него можно смотреть на p-value, или только на W? И что мне делать с результатами, как понять какой из вариантов a/b теста верный?
Цветков Максим
Общее правило по прежнему работает:
◘ Если результат p> 0.05, значит данные не отличаются от нормального распределения.
◘ Если результат р< 0,05, значит данные значительно отличаются от нормального распределения.
◘ Для
shapiro.test(data)результат вида W = 0.98134, p-value = 0.961 будет близок к нормальному распределению.Но если p-value (тестовая статистика) ≤ α: данные не соответствуют нормальному распределению + всегда нужно наносить данные на график для проверки. Графики нужны, так как при большой выборке даже малые отклонения от нормальности дадут о себе знать. Это ответ на вопрос, данные распределены симметрично или есть отложение влево/вправо.
При просмотре квантиль-квантиль для проверке нормальности важно внимательно смотреть на точки, они должны располагаться на одной линии и квантили не должны убегать за диапазон -2 и 2.
Отложения в левую сторону есть, поэтому для определения независимости выборок используется Хи-квадрат.
Альтернативная гипотеза не всегда отрицание основной гипотезы. По альтернативной гипотезе строятся правила, по которым мы отвергаем или принимаем основную гипотезу. Статистики лучше брать такие, чтобы они при альтернативной гипотезе были более экстремальны, чем при нулевой. Считаем значение статистики конкретной выборки и делаем вывод, попали ли мы в хвост распределения конкретной выборки. Если попали, значит произошло маловероятное событие и основную гипотезу отвергаем.
Обычно желаемый результат это чтобы альтернативная гипотеза была верной, в нашем случае p-value = 0.1517 выше уровня значимости 0.05. Значит мы принимаем нулевую гипотезу и заключаем, что две переменные независят друг от друга. Если расценивать два набора данных выше как количество должников за ЖКХ в Восточной Европе и Западной Европе, то принимаем гипотезу H0: среднее количество должников для двух выборок никак не связано.
Теперь сравним две независимые выборки. Можно использовать t-тесты, они сравнивают средние значения двух групп или одно среднее значение с гипотетическим средним. T-test требует нормального распределения, зависит от df (степеней свободы), и в принципе мы могли бы его использовать:
t.test(row1, row2, paired = FALSE); lm(row1 - row2 ~ 1). Но раз мы решили, что наши данные ненормальные, нам нужны непараметрические тесты. Wilcoxon или Quade нам поможет, все равно они эффективнее, чем Стьюдент.Тест противопоставляет row1 и row2, так как они независимые. В результатах смотрим на V = 52.5, p-value = 0.4374, первое это минимальная сумма рангов. Тест проверяет, что наблюдения в одной группе с вероятностью 50% больше, чем наблюдения в другой группе. Это не сравнение медиан, а сравнение средних.
P-value это накопительная величина, и на реальных проектах мы можем себе позволить ориентироваться на неё только когда она уходит в плато. Поэтому не забываем проверять выбросы в p-value по каждому дню после теста, иначе peeking problem. Peeking problem (проблема подсматривания) это когда тест уже работает, и в середине теста мы начинаем заглядывать в результаты, а вдруг уже есть статистическая значимость и можно останавливать тест. Решение: адаптивные доверительные интервалы.
Есть понятие сходимости, это как раз уходящий в плато p-value. Если количество данных, которые мы выяснили заранее для запуска эксперимента соответствует тому, что получили по факту, и статистика уже дней 5-7 в плато, то эксперимент можно закрывать.
Тут возможна ловушка: позднее закрытие теста. Есть по окончанию теста нет значимого эффекта, хочется продолжить тест. Для этого нужно уменьшать дисперсию (CUPED, вычитание предиктов, линеризация). В середине теста нельзя менять уровень значимости, целевые метрики.
Если есть вопросы по командам, то
help(t.test)иhelp(wilcox.test)могут помочь.Алексей
Здравствуйте. Статья выглядит очень полезной и умной, но все же, можно на простом примере, как проверить различия между выборками? Спасибо!
Цветков Максим
Давайте так, мы говорим про обычное сравнение групп, либо по среднему, либо по доле (более частотное). Самое сложное в тесте это дизайн теста, то есть на какую аудиторию, когда, сколько тест будет длиться, какие метрики, объем выборки, проверяется ли вообще гипотеза тестами. Самое простое это сравнение
На выходе:
prop 1 ⠀⠀⠀⠀ prop 20.08734236⠀⠀ 0.10720000
Делаем вывод, что конверсия в клики выше у лендинга 2. А
p-value = 0.0383, что меньше порогового значения 0.05, значит данные статистически значимы.Для расчета размера выборки можно пойти таким путем. Мощность обычно берут как 0.8, при огромной выборке можно и 0.99.
А вот размер эффекта не считается, а подбирается из опыта. У нас это .02, (разница между .06 и .08). Чем меньше размер эффекта, тем большая выборка нужна.
И самое сложное, а именно дизайн теста. Помимо A/B, существуют A/A/B, A/B/n, факторные, multivariate и многие другие. Multivariate test (MVT) нужен когда каждое изменение индивидуально, изолированно от других изменений, перемешивая все возможные комбинации изменений. Давайте на примере:
● Изменение A: меняем ссылки на подчеркнутые
● Изменение B: переделываем кнопки с контурных на залитые
● Изменение C: увеличиваем межстрочный интервал
● Изменение D: добавляем скелетоны
Вывод должен быть примерно таким:
● Изменение A: +3%
● Изменение B: +12%
● Изменение C: -20%
● Изменение D: +1%
Классический A/B тест показал бы 3+12-20+1 = -4%, то есть вариант со всеми правками не идет в работу. В результатах MVT должны быть и данные вида A+B= +15%, A+D = +4%, A+B+D = 16% и так далее. Но для достижения статистической значимости каждого результата потребуется тонна трафика.
Приемлемая альтернатива это factorial design. Мы тестируем множество вариантов, как в примере выше, но не все подряд. И получаем нечто вроде:
A: Изменение A = +3%
B: Изменение A + B = +15%
C: Изменение A + B + C = -17%
D: Изменение A + B + C + D = -4%
Vyacheslav Egorov
Такой вопрос. Есть результаты A/B теста, средние очень близки. Но по тестам одна выборка нормальная, а другая нет. как такие результаты интерпретировать?
Цветков Максим
От теста зависит) сравнивать средние можно, с точки зрения математики. Просто вопрос в том, что вы сравниваете? Количество ролей Николаса Кейджа и смертность от утопления после падения в бассейн, или разные значения ARPU? Для Стьюдента обе выборки должны быть нормально распределены. Можно не заморачиваться, и взять непараметрический ранговый U-критерий Манна-Уитни, если выборки независимы. Основной минус, это нулевая гипотеза сформулирована относительно медианы, а не среднего.
Либо использовать подход из мира консалтинга: берем ЦПД (должна быть большая выборка), берем из большой выборки несколько выборок поменьше, и их распределение станет нормальным.
Дементий
Отличная статья! Спасибо! Максим, не подскажете, как считать p-value при расчете bootstrap на мультивариантном тесте?
Цветков Максим
Каждый вариант сравнивается с каждым, и поправка на множественное сравнение для p-value (в итоге получится меньше, что довольно проблемно). Это из-за того, что надо не просто принять решение о победителе, а еще понять, кто из победителей самый победитель. P-value = 0,05 это ок при A/B, но уже на трех вариантах P-value = 0,025, и выборка понадобится космическая. Поэтому берутся поправки, вроде метода Бонферрони, либо лучше поправку Бенджамини-Хохберга (можно применить далеко не всегда).
Сергей
Спасибо, Максим, за статью с примерами в коде!
Пытаюсь разобраться с CUPED и постстратификацией, но не могу понять уменьшается ли дисперсия только для continous метрик.
Помогают ли эти методы в случае с обычной конверсией в покупку (binomial метрики) ?
PS Где кнопка подписаться на новые статьи?))
Цветков Максим
Чем больший период до эксперимента вы возьмете, тем меньше будет дисперсия. Чем длиннее эксперимент, тем меньше скорость уменьшения дисперсии. Но возможно, что дисперсия будет зависеть от выбора ковариата.
Вот у нас есть классический случай нехватки данных на конверсию в покупку. Пользователь пришел к нам впервые, и нет возможности собрать по нему данные до эксперимента. Значит, вводим новую ковариату (1 или 0), был ли пользователь на сайте ранее или нет. Если пользователь ранее не сайте не бывал, то задаем ковариату как любую контанту. Это аналог стратификации/семплирования, что во всех случаях ведет за собой снижение дисперсии.
Андрей Руссков
Что за множественное сравнение?
Цветков Максим
Обычно A/B-тест это сравнение двух независимых вариантов с неким уровнем значимости, скажем, 5%. Это значит, что в 5 случаях из 100 победивший вариант окажется ошибочным (ошибка первого рода).
На языке формул это будет FPR = 1-(1–0.05)¹=0.05, где метрика False Positive Rate = 1-(1-α)ⁿ. α это уровень значимости, n отвечает за количество вариантов по отношению к основному.
Итак, если мы хотим провести a/b/c-тест, то как раз встречаем проблему множественного сравнения. Сильно растет вероятность ошибки первого рода. При тестировании 10 вариантов шанс допустить ошибку первого рода аж 40%. Это фиксится коррекцией по Бонферонни. Если мы запустили тест на 10 вариантов, то с коррекцией α=0.05/10=0.005. Либо метод Холма.
Sergey
Как уменьшить кол-во FB?
Цветков Максим
Увеличить FN. Простое правило: маленький риск = мало False Positive. Высокий риск = мало False Negative.

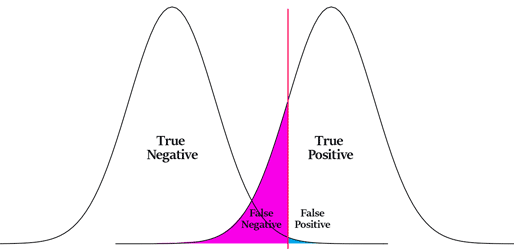
Например, проблема фишинговых писем. Тут потребуется меньше FP, потому что потенциальный вред меньше, чем потенциальные проблемы с потерей важных писем.
И наоборот, на ядерной станции лучше иметь только FP.
Andrew
Есть такая задача. В банке выдаем множество кредитов на ремонт квартиры, и резко подскачило количество досрочных поганешний. Что это может быть?
Цветков Максим
Качественно — спросить)
Количественно — сделать проверку на нормальность, и если данные нормальные, то t-test. Можно сформировать две выборки (закрыли кредит досрочно и нет), заслать в БКИ смотреть на статистически значимое различие открытых кредитов вне вашего банка после взятия кредита в вашем банке.
Vladimir Yefremov
Подскажите как считывать QQplot?
Цветков Максим
Чем больше площадь на синем графике слева, тем прямее красная линия.

Следовательно, нормальное распределение будет отображаться примерно следующим образом:
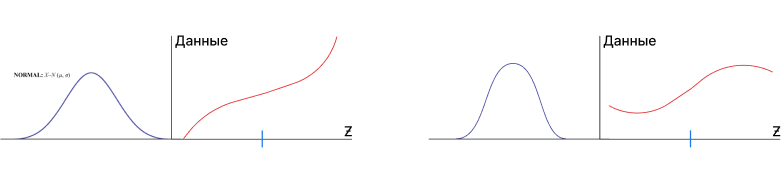
Для понимания, у гистограммы может быть длинных хвост распределения (много) и короткий (мало).
Карина
Как понять, что прокси-метрика соответствует основной метрике?
Цветков Максим
Направленность метрики это ее надежность, зачастую считают по прокси-метрике. Критерий качества прокси-метрики простой: если она согласованно повторяет траекторию изменений основной метрики, то это хорошая прокси-метрика. То есть результат двух метрик совпал -> +1. Не совпал -> -1. Если метрика очень низкочувствительная, то нужно смотреть на корреляцию t-статистик.
Метрики из метрики пирамиды, такие как North Star — либо сложно отследить, либо нужно создавать такие метрики как очень специфичные. Не «сделать мир лучше», а «кол-во новых пользователей».
Никита
Добрый день!
Подскажите как рассчитать длительность тестирования если у меня не двоичные данные и распределены они не нормально. Я как понимаю при таком случае надо проводить тест Манна Уитли, но как для него посчитать длительность не понимаю.