ANOVA и Bootstrap: проверяем UX в Python
Когда специалист научился проводить A/B-тесты, он больше не расценивает это лишь как правильный ответ на собеседовании или страшилку для разработчиков. А просто строит scatterplot, violinplot или boxplot с осознанием, что это обычный статистический эксперимент, как у социологов или медиков. Найдена волшебная кнопка «сделать хорошо», без множества перепроверок, просто рисуем графики для двух переменных. И это все? В реальной жизни задачи куда сложнее, как в анекдоте:
— Как проверить статистическую значимость моего теста?
— Могу рассказать.
— Рассказать и я могу. Как проверить?
С какими проблемами сталкиваются специалисты при проведении тестов? Мало трафика—всегда боль, если у нас в месяц 100 пользователей и 1% конверсий, а для теста нужно набрать 10 000 уников на всю совокупность. Это займет много времени, сведя выгоду от теста к нулю. Стоимость работы людей + убытки от проведения теста, и в результате выгода по результату меньше чем расходы на проверку гипотезы. Да, в интернете часто пишут, что на тест нужно 2 недели и не будет убытков. Но это цифра взята исходя из среднего времени принятия решения о покупке в некоторых отраслях бизнеса, на практике длительность проведения теста определяется не временем, а трафиком (минимально ожидаемый эффект).
Есть стандартное решение, когда мало времени на тест и слабо чувствительная метрика типа конверсии дают слабый размер эффекта. Дисперсия уменьшается с помощью CUPED и постстратификацией, но это не всегда уместно, особенно когда весь рынок это делает налево и направо. Поэтому прокси-метрики приходят на помощь, то есть связанное с основной метрикой значение, но более частотное.
Но это полбеды, результаты теста не всегда получаются с нормальным распределением. Нормальное распределение это распределение в зависимости от статистического закона (Пирсон, Байес), который указывает на равномерное распределение вероятностей по средней, а шум в данных приводит к распределению в виде кола. Если распределение скошено вправо, то медиана меньше среднего, и наоборот. Нам важна нормальность выборки: нет нормального распределения, значит, будут трудности с выбором статистического метода. Да и калькуляторы в вебе не учитывают шум в данных.
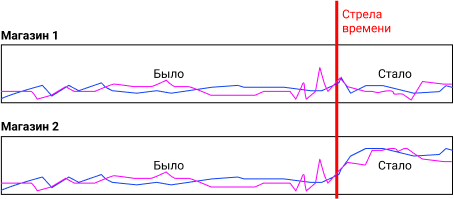
Типичная ошибка: мы не можем просто взять и сравнить рост РТО / трафика в оффлайн-магазин за счет средних по разным периодам.

Почему? На графике явно видно, что после запуска акции метрики поползли вверх. Но! Могли повлиять внешние факторы, такие как разовые выплаты пенсионерам, пришло лето, очередные новости с провокацией закупки гречки, закрылся конкурент. Решается это просто: мы делим магазины на две очень схожие группы, и делаем выводы по наличию отличий после запуска акции.
Зная про все это, мы получаем задачу на анализ A/B/C/D-теста, и искушенный множеством статей (в том числе и моих) UX-аналитик начинает попарно сравнивать все 12 гипотез t-критерием, но это ошибка использования критерия Стьюдента. Слишком велик шанс найти различия там, где их нет. Я понимаю, что на рынке любят применять Стьюдента даже на данных, очень отдаленно напоминающих нормальное распределение, но это не совсем правильно. А что мы делаем, когда у нас слишком много факторов для t-test? Мы делаем ANOVA для сравнения дисперсий. ANOVA можно применять вместо Стьюдента. Тест Стьюдента применяется, когда есть две выборки с нормальным распределением. На основе теста Стьюдента можно провести классический однофакторный дисперсионный анализ, если в тесте было более двух выборок. Раз в основе идеи лежит Стьюдент, значит и выборочные средние должны быть равны.
То есть, ANOVA хороша при любом multivariate testing, где мы тестируем изменение шрифта, формы и цвета у кнопки. Красный фон + белый текст + скругленные углы, или синий фон + желтый текст + без скруглений, или красный фон + желтый текст + без скруглений, и так далее. Это либо ANOVA, и в некоторых случаях допустимы попарные сравнения. Если по результатам теста отвергается нулевая гипотеза и нужно обозначить победителя, а у нас слишком много пар данных, то меня спасает posthocs. Например, Turkey HDS.
Суть сравнения: чем больше расстояние между нашими наборами данных, тем больше общая медиана приближена к медиане каждого отдельного набора данных.

Допустим, у вас есть 4 мобильных приложения, и в каждом продаются брендовые кроссовки разных марок. Отделу маркетинга важно знать, отличается ли средний чек этих магазинов? Проверяемой нулевой гипотезой будет предположение, что средние величины во всех выборках (т.е. 4-х группах) будут одинаковы. У нас есть две независимые переменные: трафик и набор брендов для каждого магазина. Это сложная задача, где есть аж 12 гипотез (4x). И мы должны отвергнуть нулевую гипотезу, если верна хоть одна из микро-альтернативных гипотез. Здесь сработает One-way ANOVA, в которой нулевая гипотеза (H0) это равенство средних: общая m = m1 = m2 = m3 = m4. А если результаты значимы, то мы их учитываем при принятии бизнес-решения, так как подтвержден факт о равенстве среднего чека во всех магазинах. Или мы могли найти статистически значимые отличия (H1), и дальше уже предметно смотреть, как средний чек зависит от брендов.
Рассмотрим однонаправленный и двунаправленный ANOVA. Для первого нужны нормально распределенные данные, 2 и более групп для сравнения, независимость выборок, гомогенность дисперсии. Данные распределены ненормально? Делаем на рангах, это непараметрическая ANOVA, эквивалентна Байесовским методам по результативности (но тут можно поспорить). При дискретных результатах и разном кол-ве наблюдений во множестве групп используем χ2-test (он же chi-squared test). А для анализа метрик вроде «оценка удовлетворенности» или «средний показатель завершения таски», и при разном количестве наблюдений в каждой когорте, берем ANOVA Tukey и/или post-hoc t-tests. Каким-то чудом удалось получить одинаковое количество наблюдений? Repeated-measures ANOVA и/или post-hoc t-tests.
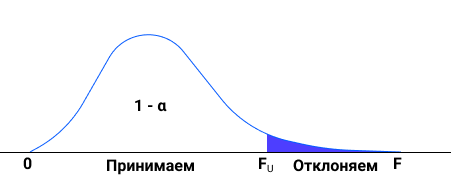
На иллюстрации ниже принцип расчета F-статистики. Это отношение между изменчивостью групп относительно друг друга и внутри каждой конкретной группы. На графике ниже два интервала, A1, A2 и B1, B2. Они пересекаются, значит нельзя сказать, что у одного среднее больше, чем у другого.
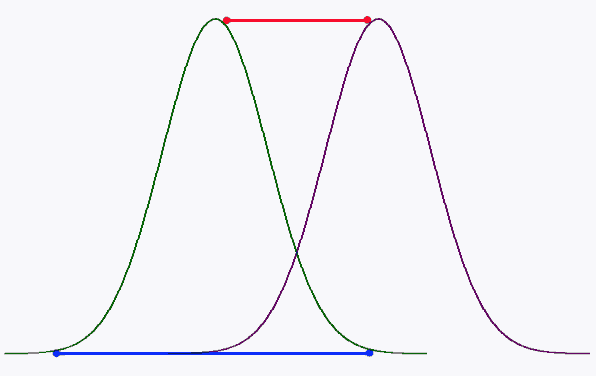
ANOVA это Analysis of Variance, или дисперционный анализ. Мы задаем вопрос: есть ли разница между всеми наблюдениями? Нулевая гипотеза: разницы нет. ANOVA это простая оценка наличия или отсутствия различий между выборочными средними. Смотрим на F-ratio и p-value, и как всегда при p ≤ 0.05 считаем, что есть отличия. Еще раз повторю: ANOVA можно применять вместо Стьюдента. Слишком много фактором для t-test? Это ANOVA, а дальше уже можно выполнять попарные сравнения. Но для этого ANOVA должна показать значимые отличия, тогда уже можно выполнять парные сравнения для точного понимания, где именно эти отличия.
И t-критерий Стьюдент, и ANOVA оценивают различия между выборочными средними. Но у ANOVA нет ограничений на количество сравниваемых средних. Даже больше, можно сравнивать больше одной независимой переменной, оценивая эффект связи между двумя или более переменными. Если устали читать и хотите уже поиграться, то вот онлайн-сервис: https://measuringu.com/ab-cal/ для N-1 2-Proportion Test.
Но для начала разберемся в теорией, взяв такой набор данных:
| Группа 1 | Группа 2 | Группа 3 |
| 4 | 8 | 2 |
| 5 | 5 | 4 |
| 7 | 3 | 6 |
Нулевая гипотеза, которая не должна устраивать менеджера продукта, это отсутствие различий между средними, и группа 1 = группа 2 = группа 3. Альтернативная гипотеза говорит, что хоть одна пара средних значимо отличается между собой.
Первый шаг это высчитывание средних значений всех наблюдений: мы суммируем все данные и делим на общее количество наблюдений: 4 +5 + 7 + 8 + 5 + 3 + 2 + 4 + 6 = 44 / 9 = 4,8. Это среднее всех наблюдений. Легко проверяется кодом d = 4,5,7,8,5,3,2,4,6 и print (statistics.mean(d)).
Следующий шаг: общая сумма квадратов (SST), насколько высока изменчивать наших данных без учета разделения их на группы. По аналогии с расчетом дисперсии, будем рассчитывать отклоенния от среднего значения. Помним, что минус на минус дают плюс:
(4 — 4,8)² + (5 — 4,8)² + (7 — 4,8)² = -0.64 + 0,04 + 4,84 = 5,25
(8 — 4,8)² + (5 — 4,8)² + (3 — 4,8)² = 10,24 + 0,04 + 3,24 = 13,52
(2 — 4,8)² + (4 — 4,8)² + (6 — 4,8)² = 7,84 + 0,64 + 1,44 = 9,92
5.259259 + 13.52 + 9.92 = 28.88 (цифры я немного округляю). Берем итоговое значение 28,88 Мы узнали значение общей изменчивости наших данных. А число степеней свободы всегда n-1, у нас суммарно наблюдений 9, поэтому df = 9-1 = 8.
Теперь рассчитываем внутригрупповую сумму квадратов (SSW), для этого высчитываем среднее по группам 4+5+7 = 16 / 3 =5,3, вторая группа 8+5+3=16 / 3 = 5,3 третья группа 2 + 4 + 6 = 12 / 3 = 4.
Давайте это проверим сразу в Python:
import matplotlib matplotlib.use('TkAgg') import pandas as pd import researchpy as rp landing_1 = [4,5,7] landing_2 = [8,5,3] landing_3 = [2,4,6] result_df = list(zip(landing_1, landing_2, landing_3)) df = pd.DataFrame(data=result_df, index=None, columns = ['set1', 'set2', 'set3']) print(df) print(rp.summary_cont(df['set1'])) print(rp.summary_cont(df['set2'])) print(rp.summary_cont(df['set3'])) |
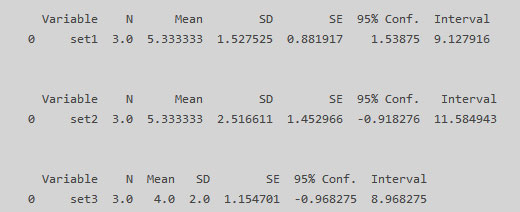
Находим отклонения элементов от среднего в рамках каждой группы, оно же SSW, сумма квадратов внутри группы:
(4 — 5,3)² + (5 — 5,3)² + (7 — 5,3)² = 1,69 + 0,09 + 2,89 = 4,66
(8 — 5,3)² + (5 — 5,3)² + (3 — 5,3)² = 7,2 + 0,09 + 5,2 = 12,66
(2 — 4)² + (4 — 4)² + (6 — 4)² = 4 + 0 + 4 = 8
Суммируем и получаем 4,66 + 12,66 + 8 = SSW 25,33, это внутригрупповая сумма квадратов. А число степеней свободы это количество всех наблюдений минус количество групп: 9-3 = 6, формула dF = N — m.
Если в ходе работе с Python вы столкнулись с проблемами, которые решаются только перезагрузкой windows, то проще сделать батник:
TASKKILL /F /IM pythonw.exe
TASKKILL /F /IM python.exe
TASKKILL /F /IM python.exe
Переходим к сумме квадратов междгрупповой (SSB), насколько групповые средние отклоняются от общего среднего: в первой группе среднее это 5,3, три элемента в группе и общегрупповое среднее 4,8. Значит, мы можем подсчитать SSB, где берем среднее одной группы и вычитаем общегрупповое среднее в квадрате, умножая все это на количество групп: 3 (5,3 — 4,8)² = 0,59, вторая 3 (5,3 — 4,8)² = 0,59 , третья 3 (4 — 4,8)² = 2,37. Все суммируем: 3,555. И число степеней свобод 3 — 1 = 2, так как dF = m — 1.
Общая сумма квадратов, или общая изменчивость = 28,88, Итак, внутригрупповая 25,33 с 6 степенями свободы, а межгрупповая 3,555 с 2 степенями свободы, значит, большая часть изменчивости обеспечивается внутригрупповой суммой квадратов. Вывод: группы незначительно различаются между собой.
И теперь мы можем подсчитать F-значение, это отношение межгрупповой изменчивости, деленное на свои степени свободы, и внутригрупповой изменчивости деленной на свои степени свободы. 25,33 / 6 = 4,2, и 3,555 / 2 = 1,7, в итоге получаем F-критерий 4,2. Итак, в числитиле 4,2 и в знаменателе 1,7 = 0.42 наш финальный ответ, это статистика. Проверим сразу двумя способами, чтобы наверняка:
import matplotlib matplotlib.use('TkAgg') import pandas as pd from scipy import stats landing_1 = [4,5,7] landing_2 = [8,5,3] landing_3 = [2,4,6] result_df = list(zip(landing_1, landing_2, landing_3)) df = pd.DataFrame(data=result_df, index=None, columns = ['set1', 'set2', 'set3']) print(df) print(stats.f_oneway(landing_1, landing_2, landing_3)) F, p = stats.f_oneway(df['set1'], df['set2'], df['set3']) print(F, p) |
Получаем два одинаковых результата: F_onewayResult(statistic=0.4210526315789474, pvalue=0.6743486572598999) и 0.4210526315789474 0.6743486572598999. Какие выводы мы можем сделать? P-value можно расценивать, как масштаб произошедшего события. P-value <0.05, значит данные статистически значимые. P-value низкий — вот и хорошо, отклоняем нулевую гипотезу и группы отличаются. Стрелочка влево это меньше, стрелочка вправо это больше. Поскольку 0.67 > 0.05 мы принимаем нулевую гипотезу. Да и 0.42 меньше 1. Данные в двух выборках может и различаются, но недостаточно.
А теперь выполним 1-way ANOVA примерно так, так это делается на реальных задачах при анализе UX, а именно используя Python. Односторонний анализ ANOVA проверяет нулевую гипотезу о том, что две или более групп имеют одинаковое среднее значение популяции. Нулевая гипотеза: средние в группах равны. Альтернативная: хоть одна средняя, да отличается. Тест применяется к двум наборам наблюдений и более, допустимы разные размеры выборок. У 1-way ANOVA может получиться только положительное F-значение. Возьмем данные по лендингам:
import matplotlib matplotlib.use('TkAgg') from scipy import stats landing_1 = [0.1533, 0.1356, 0.1764, 0.3134, 0.1817, 0.1259, 0.1344, 0.0659, 0.1923, 0.1373, 0.0724] landing_2 = [0.1745, 0.1662, 0.1672, 0.1819, 0.1749, 0.1649, 0.0835, 0.0043] landing_3 = [0.1330, 0.1352, 0.1817, 0.1016, 0.1968, 0.1064, 0.1905] landing_4 = [0.1033, 0.2741, 0.1433, 0.1677, 0.1697, 0.1636] landing_5 = [0.1522, 0.1026, 0.1733, 0.1743, 0.1339, 0.1045, 0.1835] print (stats.f_oneway(landing_1, landing_2, landing_3, landing_4, landing_5)) |
На выходе F_onewayResult(statistic=0.2843605403769587, pvalue=0.886069813400433), и 0,886 > (больше) 0,05.
Если бы мы получили р ≤ 0,05, то отклонили бы нулевую гипотезу о равенстве средних, так как существовала бы статистически значимая разница. А если 1 ≤ р <0,05, то нулевая гипотеза может быть незначительно отклонена, ведь существует незначительная разница между средними. Но у нас р > 0,05, нулевая гипотеза не может быть отклонена и разница между средними значениями не является статистически значимой. Так, 0,886 > 0,05: если p-value < 0.05, можно отвергнуть гипотезу о нормальном распределении. Мы же не отклоняем нулевую гипотезу в пользу альтернативной, средние в группах равны, средний чек в магазинах одинаковый. H0: качества всех лендингов ничем не отличаются. H1: отличия есть.
Тут все просто: нулевая гипотеза H0: set1= set2 = set3, нет существенных отличий, p_value < 0.05 позволяет отвергнуть эту гипотезу, p_value > 0.05 не позволяет ее отвергнуть.
Альтернативной гипотезой (Н1) является предположение, что по крайней мере одно среднее отличается от других. При оценке ложности H0 совершенно не важно, что послужило причиной: отличие двух или трех пар средних друг от друга. Соответственно, при подтверждении Н1 нужно чуть больше исследования данных. Давайте объединим наши данные в один dataFrame. Использованный нами ранее способ повлечет потерю части данных:
result_df = list(zip(landing_1, landing_2, landing_3, landing_4, landing_5)) df = pd.DataFrame(data=result_df, index=None, columns = ['set1', 'set2', 'set3', 'set4', 'set5']) |
Поэтому поступим чуть более хитро, и сразу же нарисуем boxplot:
df = pd.DataFrame({'landing_1': pd.Series(landing_1), 'landing_2': pd.Series(landing_2), 'landing_3': pd.Series(landing_3), 'landing_4': pd.Series(landing_4), 'landing_5': pd.Series(landing_5)}) print(df) df.boxplot(column=['landing_1', 'landing_2', 'landing_3', 'landing_4', 'landing_5'], grid=False) plt.show() |
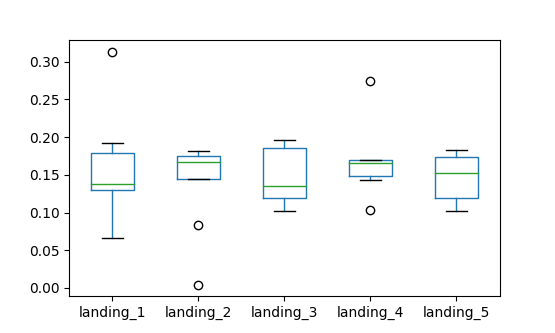
Видим серьезные выбросы, еще немного визуализируем и убедимся, что некоторые лендинги вытягиваются выбросами.
plt.hist(landing_1, alpha=0.5, label='landing_1') plt.hist(landing_2, alpha=0.5, label='landing_2') plt.hist(landing_3, alpha=0.5, label='landing_3') plt.hist(landing_4, alpha=0.5, label='landing_4') plt.hist(landing_5, alpha=0.5, label='landing_5') plt.legend(df) plt.show() |
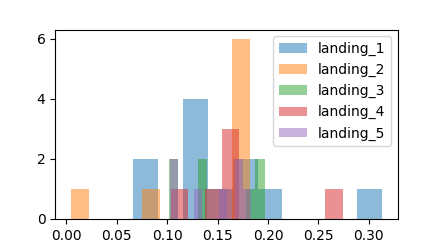
Сравнивая средние, вы можете заметить, что одна группа определенно лучше других (в данном случае хочется оставить landing_1 и landing_2). И именно по такому графику часто ошибочно выбирают победивший вариант, а он победил просто за счет выбросов. В этот момент сразу отключаем технаря и включаем дизайнера/аналитика с вопросами: а не скопили ли мы бренды с лучшим соотношением цены/качество в одном магазине? Аффектили ли результаты сезонные акции? А вдруг в выборке половина наблюдений это покупки через агрегатор, и этот фактор перекрыл качество дизайна?
В итоге, одностороннюю ANOVA можно легко выполнить командойprint(stats.f_oneway(landing_1, landing_2, landing_3, landing_4, landing_5)). Если P > (больше) 0,05, то с большой долей уверенности можно утверждать, что средние значения результатов всех выборок существенно не отличаются. И дальше уже исследуем данные более привычными способами. Вас устроил такой сумбурный результат? Вы могли заметить, у нас в данных присутствуют выбросы и уж слишком не одинаковое количество наблюдений, я сделал это умышленно. В таком случае лучше применять дисперсионный анализ по Краскелу-Уоллису/Kruskal-Wallis H-test и Welch’s ANOVA. Это непараметрические аналоги ANOVA. Используются в качестве замены параметрического одностороннего ANOVA, когда допущения этого теста серьезно нарушаются. Kruskal-Wallis test не предполагает ни нормальности популяции, ни однородности дисперсии, как и параметрическая ANOVA, и требует только упорядоченного масштабирования зависимой переменной. Kruskal-Wallis используется, когда нарушения нормальности популяции и/или однородности дисперсии являются экстремальными. Поскольку дисперсионный анализ по Kruskal-Wallis относится к группе непараметрических методов статистики, это значит, что при выполнении соответствующих расчетов параметры того или иного вероятностного распределения (например, нормального) никак не задействованы. Вместо этого используются ранги исходных значений и их суммы в сравниваемых группах. Давайте выполнил этот тест на тех же данных, помня, что нулевая гипотеза про равенство средних:
import matplotlib matplotlib.use('TkAgg') from scipy import stats print (stats.kruskal(landing_1, landing_2, landing_3, landing_4, landing_5)) |
Результат KruskalResult(statistic=0.2731503574200107, pvalue=0.9914808283052362). Надо p-value ≤ 0,05. «Различия между некоторыми медианами статистически значимы»— это то, что менеджер ожидает от нас получить. Но наше p-value=0,991, а 0,991 > 0,05, значит, срабатывает правило P-value > 0,05: различия между медианами не являются статистически значимыми. Мы НЕ можем опровергнуть нулевую гипотезу о том, что все медианы групп равны. Заключаем, что средние равны.
Так, по Краскелу-Уоллису 0,991 > 0,05 и по ANOVA 0,886 > 0,05. Нулевая гипотеза про равенство средних. Разница между средними значениями не является статистически значимой, принимаем нулевую гипотезу.
Мы не считаем результаты теста достоверными, нет победителя среди вариантов, они одинаковые.
Напомню, что статистическая значимость это показатель, позволяющий нам понять, являются ли результаты теста закономерностью или случайностью, с точностью 95%.
Давайте рассмотрим другой пример:
import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt from numpy.random import seed import numpy as np import random from scipy import stats seed(1234) alpha = 0.05 true_cov = np.array([[.8, .0, .2, .0], [.0, .4, .0, .0], [.2, .0, .3, .1], [.0, .0, .1, .7]]) random.shuffle(true_cov) landing_1 = np.random.multivariate_normal(mean=[.8, .0, .2, .65], cov=true_cov *np.eye(4), size=140) landing_2 = np.random.multivariate_normal(mean=[.4, .0, .2, .0], cov=true_cov *np.eye(4), size=140) landing_3 = np.random.multivariate_normal(mean=[.6, .0, .2, .21], cov=true_cov *np.eye(4), size=140) landing_4 = np.random.multivariate_normal(mean=[.4, .1, .2, .0], cov=true_cov *np.eye(4), size=140) landing_5 = np.random.multivariate_normal(mean=[.8, .0, .2, .05], cov=true_cov *np.eye(4), size=140) stat, p = stats.kruskal(landing_1,landing_2,landing_3,landing_4,landing_5) print('Statistics=%.3f, p=%.3f' % (stat, p)) print (plt.plot(landing_1,landing_2,landing_3,landing_4,landing_5)) if p > alpha: print('Распределение одинаковое (не отклоняем H0)') else: print('Распределение разное (отклоняем H0)') |
Statistics=43287.107, p=0.000, такой p-value годится не просто для лендингов, с ним можно запускать в эксплуатацию атомный реактор, трейдинговую систему или искусственный интеллект (после Байеса, а частотный подход это физика, психология). Аналогично, опровержение нулевой гипотезы не указывает на то, какая из групп отличается. Если p > (больше) 0,05, то между группами не наблюдались статистически значимые различия. Здесь же срабатывает правило P < (меньше) 0,05, различия между средними являются статистически значимыми, мы отклоняем нулевую гипотезу про равенство всех медиан. Если p-value равно 0.00, у нас есть основания отвергнуть нулевую гипотезу на уровне значимости 5% (0.00 < 0.05), но нет оснований отвергнуть ее на уровне значимости 1% (0.001 > 0.0001). Тут важно понимать, что у нас нет оснований не только отвергнуть, но и принять нулевую гипотезу. В условии задачи речь про «вероятность отвергнуть нулевую гипотезу», про альтернативную гипотезу ни слова.
Two-Way ANOVA: вернемся к примеру с четверкой магазинов брендовой обуви. Магазины очень схожи по ассортиментной матрице, по поисковой выдаче. А если нужно сравнить продажи в магазинах, которые отличаются по рейтингу в Рамблере, и одновреенно по дизайну как по доминирующему фактору? Или наличие интерактивного чата на одном из сайтов дополнительно влияет на конверсию? Для этого нужна двусторонняя ANOVA. Этот критерий исследует влияние одной или нескольких категорий независимых переменных, известных как «факторы», на зависимую переменную. Двусторонняя ANOVA, как и все ановы, предполагает, что наблюдения нормально распределены. И мы хотим проверить с помощью двусторонней ANOVA влияние двух переменных (место в рейтинге Рамблера и разный дизайн) на продажи через сайты.
Мы будем использовать библиотеку pingouin, обратите внимание, что она работает минимум с версией Python 3.5. Библиотека очень хорошая, только посмотрите, как много полезной информации она возвращает при простом t-test.
import matplotlib matplotlib.use('TkAgg') import numpy as np import pingouin as pg np.random.seed(44) mean, cov, n = [0, 0], [(2, .6), (.92, 1)], 30 x, y = np.random.multivariate_normal(mean, cov, n).T print (pg.ttest(x, y)) |

Я предпочитаю использовать pingouin вместо pyvttbl, так как последний практически перестал поддерживаться. Проведем двусторонний тест, для начала подготовим данные:
import matplotlib matplotlib.use('TkAgg') import pandas as pd data = pd.read_excel (r'E:\Python_2\Book1.xlsx') df = pd.DataFrame(data) print (df) |
Укажем аргументы: dv это название столбца, содержащего зависимые переменные, between это столбец, содержащий коэффициент между группами.
import pingouin as pg from statsmodels.graphics.factorplots import interaction_plot fig = interaction_plot(df.Rambler, df.Design, df.Result, ms=8) aov = pg.anova(dv='Result', between=['Rambler', 'Design'], data=data, detailed=True) print(aov) |
Source SS DF MS F p-unc np2
0 Rambler 5.757415e+06 3.0 1919138.223 1.885 0.147555 0.124
1 Design 1.647162e+05 3.0 54905.413 0.054 0.983255 0.004
2 Rambler * Design 4.878005e+06 9.0 542000.585 0.532 0.842054 0.107
3 Residual 4.071443e+07 40.0 1017860.875 NaN NaN NaNВ первую очередь смотрим на p-value, и если только принимаем нулевую гипотезу, то только тогда смотрим на f-value. Нет существенного влияния рейтинга в Рамблере на предпочтения аудитории. Поскольку р-значение намного выше порога статистической значимости (0,05), можно сделать вывод, что все три эффекта вместе взятые не оказывают значительное влияние на продажи с лендингов. Оба фактора влияют на количество продаж, однако их взаимодействие значимым не является.
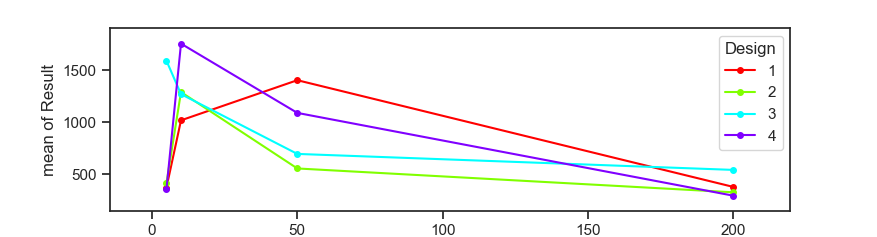
Хотя экспертно я бы сказал, что лендинги в каталоге рамблера на позициях до 50 отрабатывают значительно лучше, чем когда они находились на более дальних позициях.
Есть две школы, Фишера (Anova, p-value, нулевая гипотеза, непрерывная мера) и Нейман/Пирсон (PCA, метод моментов, хи-квадрат).
Bootstrap, интервалы и A/B-тест
Мы много поговорили про дисперсионный анализ (ANOVA) как способ тестирования равенства средних. Можно смотреть и в сторону альтернатив, таких как Welch’s t-test или Mann Whitney-Wilcoxon. Но всегда ли они уместны? Нет, на реальных задачах может вылезти показатель с гетероскедастичностью (решается делением у на x).
На минуту вернемся к основам. Статистика это измеримая функция от выборки. Выборка: X = {X1,….., Xn}. Например, вот статистика выборочного среднего:

Предположим, у нас есть нормальное распределение (f0), оно легко дифференцируемо, и нам нужно оценить математическое ожидание распределения. Один из вариантов это метод максимального правдоподобия. Выписываем функцию и максимизируем ее по параметру. Можно взять логарифм, а так как он монотонный, то точка экстремума не меняется.
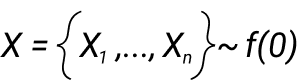
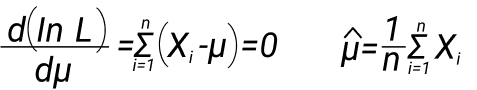
Этот пример вы можете найти практически в любой книге. Но что, если наша плотность это совокупность нормальных распределений? Или от нас требуется узнать дисперсию оценки? Тут уже точечные оценки дают сбой. Приходит на выручку эмпирическая функция распределения, в частности, bootstrap.
Допустим, у нас есть множество наблюдений с неизвестным распределением. Мы можем подсмотреть распределение из медианы. Но хороший ли это подход? Если все данные в выборке очень близки к 50, то и медиана будет близка к 50. Но если одна половина наблюдений близки к 0, а вторая половина близка к 100, то мы не можем быть уверены в медиане. Как же быть? Все перепроверить множество раз. Рассмотрим нахождение доверительных интервалов. Если нет желания возиться с Байесом и нужны нормальные результаты, то используем Bootstrap. У Bootstrap есть минус, его мощность меньше, чем у параметрических критериев, но мы это будем решать большим объемом выборки. А если у вас ненормальное распределение данных, то Bootstrap это самый лучший способ нахождения доверительных интервалов, так как метод непараметрический.
- У нас есть выборка размера n, из которой семплируется выборка аналогичного размера множество раз (B). Новая выборка это x.
- Вычисляем значения:
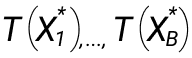
3. Высчитываем оценку функционала по bootstrap T(F):
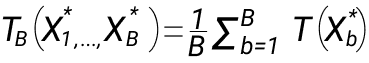
4. Выччисляем выборочную дисперсию по набору значений, и дальше уже работаем с ней:
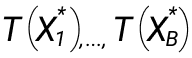
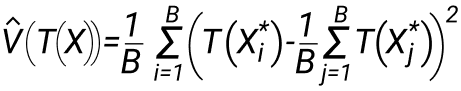
Сразу отметим, что если у вас огромное количество данных, на уровне Яндекса, Касперского или Авито, то Bootstrap вам не подойдет. Будет слишком медленным. Ваш выбор это линеаризация. Остальные могут использовать Bootstrap. Но! Bootstrap также не очень хорошо работает, когда в выборке много аномальных значений или попросту мало данных. Если изначальные данные искажены, то и результат работы Bootstrap будет искажен.
Предположим, что у нас есть треугольное распределение, при котором закон распределения не совсем очевиден. Построим теоретическую, эмпирическую и функцию распределения от bootstrap.
import numpy as np import matplotlib.pyplot as plt %matplotlib inline def MakeDistrubition(x): if x < 0: return 0 elif x < 1: return x**2 / 2 elif x < 2: return 2*x - x**2 / 2 - 1 else: return 1 size = 400 X = np.random.uniform(0,1, size=size) + np.random.uniform(0,1,size=size) Len = len(X) B = 1 defacto = np.random.choice(X, (B,Len), replace=True) defacto.shape plt.figure(figsize= (20,12)) for bootstrap_sample in defacto: plt.hist(bootstrap_sample, bins=Len, density=1, histtype='barstacked', cumulative=True, alpha=0.15, color='black', linewidth=2) plt.plot (np.linspace(0,2,400), list(map(MakeDistrubition, np.linspace(0,2,400))), color = "magenta", label = "True", linewidth = 3) plt.hist(X, bins = Len, density=1, histtype='step', cumulative = True, label = "Empirical", bottom=None, color = 'green', linewidth = 3) plt.legend() plt.show() |
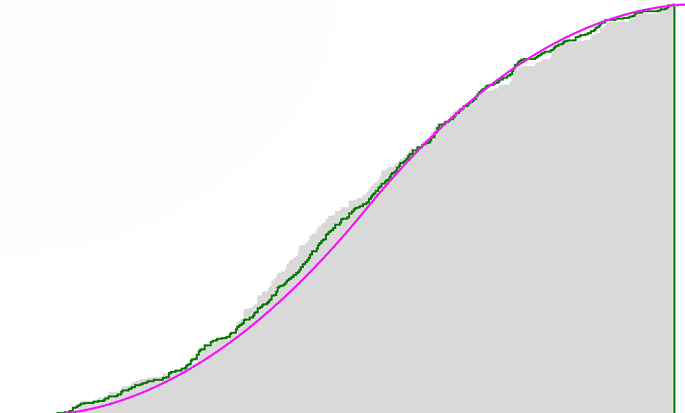
Видно, что теоретическая и эмперическая функции очень схожи. Можно сделать вывод, что доверительные интервалы имеют негативные и позитивные сценарии (нижняя и верхняя границы интервала). Если мы увеличим размер выборки, то эмпирическая функция распределения станет очень похожа на теоретическую.
Параметрический Bootstrap работает с неким параметром распределения, из которого формируется выборка с умеренной дисперсией. А еще есть непараметрический Bootstrap, который не полагается на параметр, а просто оптимизируем сдвиг от среднего.
Принцип работы: Bootstrap работает по принципу ресемплинга выборки с возвратами. Относится к семейству методов Монте-Карло, генераторы случайных чисел. Есть исходные данные, мы берем оттуда n-количество наблюдений, рассчитываем во взятом наборе некую статистику, например среднее, и кладем обратно. Это называется семплированием, когда мы получаем выборку из данных и анализируем только эту выборку. И повторяем это много раз. Тем самым мы получаем среднее с некой величиной отклонения от среднего. Критерии качества работы Bootstrap это форма рапределения бут-статистики (унимодальность), и чем меньше bias, тем лучше.
Виды семплирования можно разделить на два блока: случайные и детерминированные. С первыми все понятно, случайным образом берем значения из выборки. Детерминированные про некую систему, например, брать каждые два значения через пять значений. Bootstrap в основном работает со случайным семплированием, не стесняясь ресемплинга. То есть, возможна ситуация, когда из набора значений 1,2,3,4,5 получится выборка 1,3,3,3, выбранное значение будет возвращено в изначальный набор данных и может быть взято повторно.
Если у вас выбора в пару миллиардов значений, то постоянно семплировать с возвратами это очень тяжелая операция. Если вам так повезло с объемом данных, то можно применять метод бакетов. По каждому бакету считается среднее, и сравниваем распределение двух средних.
Доверительный интервал можно рассчитывать разными способами, Bootstrap лишь один из них, он не требует никакой нормальности данных и даже допускает неточность результатов, так как ЦПТ. На примере правила трех сигм, нужно отложить квантили уровня 2α и 1-2α, и это будут наши доверительные интервалы, в рамках которых можно отклонить нулевую гипотезу.
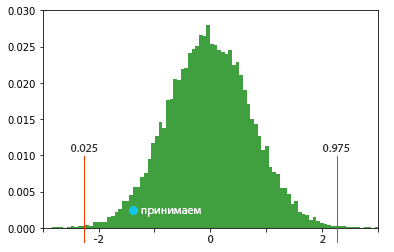
Один из способов нахождения доверительного интервала с помощью bootstrap это нормальный интервал, но он требует выполнения условий ЦПД. Но я рекоменую смотреть в сторону центрального интервала, или на интервал на основе перцентилей.
Попробуем получить вектор из значений после bootstrap из нормального распределения.
import numpy as np np.random.seed(45) X = np.random.normal(20, 2, 200) def theta(input): return np.exp(np.mean(input)) def bootstrap (input, function, n_times = 500000, random_state=15): np.random.seed(random_state) bts_statistics = np.empty(n_times) for i in range(n_times): input_b = np.random.choice(input, size=input.size) bts_statistics[i] = function(input_b) return bts_statistics theta_estimate = theta(X) theta_bootstrap_estimate = bootstrap(X, theta) print (theta_bootstrap_estimate) |
На выходе у нас следующий вектор: [4.47464000e+08 4.11481479e+08 4.13320475e+08 ... 4.68092497e+08 5.01441718e+08 5.58717285e+08].
Для Bootstrap лучше скопить минимум 10 000 наблюдений, а при адекватных требованиях к точности 15 000, хоть это и скушает ресурсов компьютера при расчете. Если у вас 100 наблюдений, лучше выбрать более точный метод для оценки доверительных интервалов. Тот же тест Monte Carlo весьма точен, а Bootstrap нет, и тут вы захотите отказаться от Bootstrap и закрыть статью. Bootstrap это ведь всего лишь непараметрический метода для оценки неизвестного количества выборочных распределений, таких как дисперсия, смещение, процентили. Но для Monte Carlo придется смириться с допущениями в распределении. Для Bootstrap достаточно взять большую выборку, и достоверность подрастет, с возможностью применения на широкий спектр гипотез, а не просто H1 vs. H2 vs. H3. Просто задать количество семплов/бакетов от 1000, тогда точность сойдется благодаря закону больших чисел. Идея простая: bootstrap бывает параметрический и непараметрический. Непараметрический работает с эвристикой, без предположений.
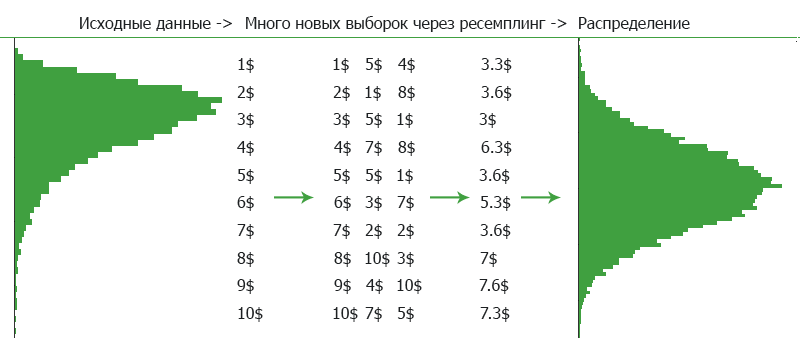
Но! это не нормализация данных.
Что такое доверительный интервал? Это некий допустимый зазор. Внутри этого зазора есть истинное среднее значение для всей популяции. Видите здесь p-value? Нет, он тут и не нужен, так как можно рассматривать доверительные интервалы как p-value.
Суть доверительного интервала: система нам выдала доверительный интервал 14,5 и 28,5, это некий диапазон значений. У нас значение n=20, и чем более узкий доверительный интервал, тем лучше. Напомню, что 90% — 1.645, 95% — 1.96, 99% — 2.575. Часто принимают некую переменную n за диапазон от -1 до 1, d диапазон от -2 до 2, y это от -3 до 3, и отсюда начинается поиск доверительной вероятности. Описанные выше числа 90, 95, 99 то это как раз доверительный интервалы.
Работаем ручками. В SciPy нет встроенного Bootstrap, нужно установить scikits.bootstrap.
import matplotlib matplotlib.use('TkAgg') from scipy import stats import scipy import scikits.bootstrap as bootstrap from matplotlib import pyplot as plt data = stats.poisson.rvs(33, size=15000) results = bootstrap.ci(data=data, statfunction=scipy.mean) print (results) plt.plot(data, '.') plt.waitforbuttonpress() plt.show() |
Мы получили симпатичный график, но что важнее, у нас 2 границы интервала: от 32.9208 до 33.10533333. Это нижняя и верхняя границы диапазона. Полученный интервал не включает 0, делаем вывод, что изменение конверсии статистически значимое. Создадим новое распределение:
plt.figure(figsize = (14,7)) x = np.concatenate([np.random.exponential(size=600), np.random.normal(size=600)]) plt.hist(x, 35, histtype="step", linewidth=1, density=True); |
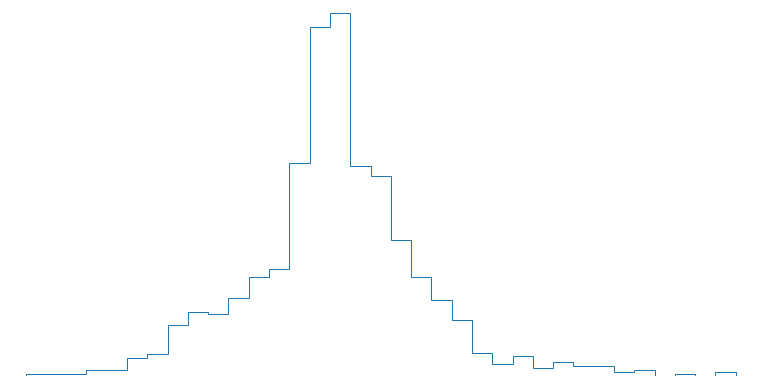
И нам дали задание узнать, в каком диапазоне лежит среднее с достаточной долей вероятности и какова точечная оценка. Решение следующее:
n = len(x) B = 100000 ranc = np.random.choice(x, (n,B)) mb = ranc.mean(axis = 0) mb.shape intervals = np.percentile(mb, [1.5, 98.5]) print (intervals) np.mean(x) |
Получаем [0.36265025 0.49580532] и 0.42921685831404904. Результаты на основе дисперсии, это важно понимать. Эмпирическая функция распределения близка к теоретической, на это мы и делаем упор.
Какую задачу мы решаем: у нас есть два варианта главной страницы сайта из A/B теста. Первую версию сайта увидели 3700 пользователей (set1) с конверсией в покупку 4% (money1). Вторую 3700 (set2) и сконвертились 6% (money2). Предположим, что пользователи одинаковые и никакие другие факторы не влияют на наши результаты. Был ли рост конверсии в покупку на второй версии или рост конверсии в покупку с 4% до 6% может быть случайностью? Считаем доверительный интервал для разницы двух конверсий, получая некий диапазон. Получаем две границы интервала: -0.0323 и 0.0323. Полученный доверительный интервал расцениваем так: с вероятностью 95% разница реальных конверсий в покупку между двумя лендингами лежит в интервале от -0.0323 % до 0.0323%. В этих результатах есть 0, и мы считаем, что изменение конверсии лендингов не значимые. Изменения могли быть вызваны не результатами наших продуктовых решений, а любой случайностью: погодой, сбоем связи у провайдера или изменением алгоритмов поисковой выдачи.
Сделаем чуть по другому: возьмем две версии главной страницы сайта и проверим, насколько значимыми могут быть изменения. Мы можем нагенерировать из полученной выборки нужное количество значений, и вычислить среднее значение для каждой выборки. В этот раз я использую другую бибилотеку, bootstrapped.
После использования любого метода сравнения групп (ANOVA в этой статье), используем бутстреп с ограничением на размер семплированной выборки. Если с выборкой переборщить, то хи-квадрат гарантированно даст значимые различия, я бы предпочел на огромной выборке просто смотреть средние/медианы. Общее правило: t-критерий нужен для интервальных данных, а хи-квадрат для биномиальных/категориальных. Менее наглядный, так как считать среднее и дисперсию становится бессмысленно.
import numpy as np import bootstrapped.bootstrap as bs import bootstrapped.stats_functions as bs_stats mean = 354 stdev = 20 population = np.random.normal(loc=mean, scale=stdev, size=15000) samples = population[:2000] print(bs.bootstrap(samples, stat_func=bs_stats.mean)) print(bs.bootstrap(samples, stat_func=bs_stats.std)) |
Что получаем: медиану 354.58365523949504 (353.7118039181707, 355.4594831931443) и стандартное отклонение 19.735458244752863 (19.107225523688825, 20.357779620637967). Теперь мы понимаем, насколько средние значения из подгруженных данных соответствуют среднему общему значению. Значения можно интерпретировать так: среднее время, проведенное на сайте, примерно одинаковое.
Стандартное отклонение это значение в натуральных единицах отклонения на одну сигму. Минимальное возможное значение для стандартного отклонения это ноль, и то когда в наборе данных отклонений нет. То есть набор данных выглядит так: 24, 24, 24, 24, 24, 24 и еще тысячи 24. Хороший вариант: 1,2,3,3,4,5,6,7, где среднее 4 и стандартное отклонение ≈2. Похуже: 1,2,3,4,5,6,100, где среднее 17 и стандартное отклонение ≈36. Медиана же в обоих случаях будет равна 4, но стандартное отклонение будет сильно различаться.
Я использую Bootstrap, когда встречаю смешанные распределения. Или когда надо симулировать выборочное среднее, так как возможность поработать со 100% объемом данных появляется примерно раз в никогда. А вот задачи регрессии и аппроксимации Bootstrap не под силу. Да и уступает по мощности параметрическим тестам.
Nota bene: цифры всего не скажут.

24 комментария
Ivan Popelyshev
Здравствуйте!
Можете подсказать: у нас есть данные по конверсии по одному магазину (как раз магазин обуви), как в статье. Мы решили давать дополнительные скидки клиентам, которые уже купили товар. Уже скопили новые данные, конверсию по акции. Как теперь сравнивать такой A/B тест? Спасибо!
Цветков Максим
Технически, это не A/B. A и B не должны быть взаимосвязанными событиями. У вас же задача про вероятность наступления события B при наступлении события A. Вам нужен Байес.
Max Polonski
Перечитал все, что у вас написано в блоге, многое полезно! Но не смог найти критерий для следующей ситуации: кастомер заказывает машину утром и вечером, это дает нам два пика в течении суток. Или заказывает еду 4 раза в день в примерно одинаковое время, получается 4 пика. И это повторяется каждый день, значит вероятность должна быть плавно зацикленной на двух концах 23:59 и 00:00. Какой критерий используется для таких ситуаций?
Цветков Максим
Задача на нахождение плотности вероятности бимодальных данных. Ну
t-mean/stdточно не подойдет, нужна классическая смесь распределения Фон Мизеса, сутки можно представить как замкнутый круг.Ярослав Макаров
Здравствуйте, есть обычный A/B тест с разными системами рекомендаций по покупке, и по числу покупок есть победитель. Для доказательства неслучайности результатов мне нужен бутрстап, правильно?
Цветков Максим
Если нужно получить результат быстро, то bootstrap. Суть описана в статье, но если вкратце: для каждой выборки выбираем клиентов 500-1000-2000 раз, на каждый раз считаем среднее, отсекаем 2.5% крайних малых и больших значений, получаем 95%-доверительные интервалы. Получаем доверительный интервалы и смотрим пересечение. Либо сложнее, t.test для нормальных данных, для остальных типов распределения wilcoxon с conf.int = TRUE для доверительных интервалов.
Saida Kladkov
Здравствуйте, можете рассказать как делать классификацию? Я понимаю, что можно разбивать наборы данных на некие группы по признаку, от более общей категории к более конкретной. Но не очень понимаю суть этого процесса.
Цветков Максим
В задачах классификации и регрессии применяются деревья решений. Если речь идет о бинарных деревьях (один узел делится на две части), то происходит переход по левому ребру по истинному условию, и по правому ребру по ложному. Признаки могут быть числовые и категориальные. Давайте на примере с категориальным. Берем критерий разбиения (энтропия Шеннона) или более простой индекс Джини, критерий создается при создании случайного леса. Критерий можно придумать самостоятельно. Мы берем все признаки, по каждому признаку смотрим, где признак Джини минимальный, и делаем разбиение. Вот пример данных:
Принцип разбиения такой:
y[x > 1000]если цена меньше 1000₽, те значения, которые больше, идут в правое поддерево, а в левое поддерево идут меньшие значения. В верхней части дерева обычно прописывают очень простые условия, Обычно это сравнение значения одного из признаков x*j с некоторым заданным порогом t: x*j ≤ t.Это довольно стандартное действие для массива NumPy: знак >= уводит нас в правое поддерево, знак < в левое. Теперь поймем, сколько значений пойдет в правое поддерево.
len(y[x >= 33] == 1), получаем 16. Суть написанного кода: x больше или равно 33, а y = 1. Для примера я вписал 33 как порог, на практике мы бы перебирали все решения и выясняли для каждого из значений индекс, он же критерий Джини. Вот так можно понять, куда какие значения уйдут.Далее все это можно вынести в функцию с индексом Джини. Функция нужна только для частного случая, когда некое значение больше выбранного нами порога, относим его к классу 1, а то значение, что меньше, к классу 0. Из явных косяков такого подхода, это если хоть одно поддерево пустое, то будет деление на ноль и будет ошибка, поэтому оба дерева в данной реализации должны быть обязательно заполнены. И у нас два класса, нет смысла разбивать на три поддерева.
В результате у нас три значения, 6, 10 и 0.234375, последнее это индекс Джини. В данных выше третий признак это зарплата, второй это опыт работы, и четвертый признак — уровень квалификации. И там, где индекс Джини минимальный, делаем первое разбиение, находим выгодный предикат, который наиболее удачно будет раскидывать данные на две векти, и далее решение уточняется новыми предикатами.
Это можно еще и циклом вывести:
Граница:57.0, gini=0.37038286388935737
Граница:87.0, gini=0.44437499999999996
Граница:34.0, gini=0.234375
Граница:12.0, gini=nan
Граница:43.0, gini=0.41709183673469385
Граница:87.0, gini=0.44437499999999996
Граница:46.0, gini=0.3819444444444444
Граница:69.0, gini=0.359375
Граница:141.0, gini=0.4444444444444445
Граница:144.0, gini=0.2283737024221453
Граница:45.0, gini=0.3966863905325444
Граница:12.0, gini=nan
Граница:94.0, gini=0.4530177514792899
Граница:38.0, gini=0.4444444444444445
Граница:91.0, gini=0.4444444444444445
Граница:74.0, gini=0.41975308641975306
Граница:121.0, gini=0.45408163265306123
Граница:141.0, gini=0.4444444444444445
Sasha Zolotarev
Здорово! Хорошее объяснение, а в финтехе используетсяя дерево, или сразу много таких деревьев?
Цветков Максим
Из таких вот деревьев может состоять целый лес. И тут как раз пригодится бутстреппинг. Еще раз принцип: у нас есть несколько наблюдений, [1,2,3,4,5], в результате работы Bootstrap мы получаем аналогичный набор данных. Если сделать два возврата, то получим такие датасеты [1,5,3,3,5] и [2,1,4,2,2]. Порядок здесь не важен, мы видим что отсутствуют некоторые наблюдения, зато во второй выборке цифра 2 фигурирует аж три раза. Таких выборок можно сделать много, и на каждой запускать свое дерево решений. И возникает вопрос, а какому дереву верить? Решается голосованием. Мы взяли некие данные, и получили классы вида 0,0,1,1, на втором дереве 0,1,1,0, на третьем 0,0,1,0. Мы видим, где решения совпадают, и получаем итоговый результат 0,0,1,0, примерно так и работает лес. У случайного леса те же преимущества, что и у деревьев: 1. данные можно не нормализовать, 2.дереву без разницы, какие признаки, 3. масштаб признака не важен. Масштабирование признаков очень слабо влияет на случайный лес, а если мы будем менять целевую переменную (Y), масштабировать или логарифмировать, то линейная модель сломается. Даже если в случайном лесе пара деревьев слишком переобучатся, другие деревья все равно сгладят результаты. Минусы случайного леса: модель сложная, отсюда проблемы с обоснованием, интерпретацией, так как это черный ящик. Очень сложно объяснить бизнесу и клиентам бизнеса, что у нас глубина 10 и 30 признаков (очень много узлов), и поэтому одному клиенту можно выдать кредит, а другому нельзя.
В разных библиотеках случайный лес реализован по разному. Поэтому отслеживаем, чтобы во всем случайном лесе использовались все признаки. Если часть данных после Bootstrap не попадает в подвыборку, то значит они и не попадают в обучение, это называется Out-of-bag (OOB) error. Так как у нас ансамбль, то можно выбрать количество деревьев, в scikit-learn количество деревьев по умолчанию от версии к версии меняется. Количество ядер тоже можно выбирать. В идеале, для всего этого нужно писать библиотеку на С и запускать в Python.
Василий Иванович
Привет! круто, а как принято мониторить качество модели? Есть модель предсказания спроса в магазине, и метрика AUC ROC (хотя не уверен, что понимаю эту метрику). Хочу отправить модель на прод, какая на проде будет метрика?
Цветков Максим
Классические a/b тесты + контрольная группа. Только после того, как метрики прошли DS-испытания. Мониторим то, на что влияет модель, + PSI (Population Stability Index) на признаки. Сравнивать статистики по признакам, меняется ли среднее, максимум, смотреть распределение предсказаний.
Смотрите, принцип работы ROC-кривой хорошо можно увидеть на картинке, на которой отложены true positive rate и false positive rate. Красная линия это подбрасывание монетки, вероятность 50/50, то есть глупая модель. Линия выше диагонали это лучше, чем пальцем в небо. Метрики TNR и TPR. И по фиолетовой линии можно смотреть, что если мы хотим закрывать 90% тикетов автоматически, то мы соглашаемся на 2% ошибок.
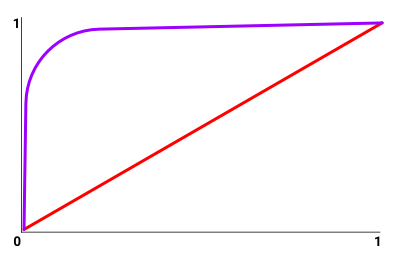
Площадь под ROC-кривой надо толкать в верхний левый угол.
Василий Иванович
Выглядит разумно. А если без a/b? например, оценить маркетинговые акции?
Цветков Максим
Тогда CausalImpact, если есть две коррелирующие метрики и стационарные данные. Или fbprophet, байесовская статистика, где регрессоры это отдельные акции, + другие факторы. Есть поддержка работы с праздниками, сезонностью. Либо arima, survival/hazard.
Простой способ это использовать GA Effect.
Kate Filatova
Очень много критериев. Как выбрать правильный?
Цветков Максим
Либо эмпирически на моделируемых экспериментах (мой выбор), либо академически, по книгам и научным работам. Книги и научные работы иногда друг другу противоречат.
1) Берем сырые данные
2) Разбиваем выборку на две группы
3) Прогоняем данные на реальном тесте
4) Моделируем тест 2-3 тысячи раз
5) Смотрим результаты и FPR (False Positive Rate) через множественные AA-тесты.
Lev Bolshakov
Привет! как добиться нормального сплитования выборок?
Цветков Максим
Для проверки нужно запускать еще и A/A-тест, где не оказывается никакого воздействия. Если вдруг находятся статистически значимые различия в таком тесте, значит проблема в сплитовании. Можно взять данные за исторический период. Далее тестом Колмогорова-Смирнова проверить принадлежность распределения к определенному семейству.
Процесс такой:
1) данные нужно очистить от мусора.
2) выбор типа метрики (бинарные (0/1), непрерывная, метрики отношений).
3) для принятия решения о том, какая группа лучше, используются статистические критерии для оценки разных метрик. Обычно это непараметрический bootstrap для метрик отношений + CUPED для увеличения чувствительности метрики.
Serg
Добрый день. В статье рассматривались случаи нормальных распределений. У меня есть несколько результатов тестов, гистограмма по которым показывает логнормальное распределение. Вопрос: есть ли тесты на «похожесть » распределений для логнормальных или мне необходимо сначала самому логарифмировать результаты и превратить свои распределения в нормальные, а потом строить, например, ANOVA?
Спасибо.
Цветков Максим
Логарифмирование не всегда помогает, в некоторых случаях даже немного вредит. И после логарифмирования меняется интерпретация. Не все распределения нужно сводить к [-1; 1].
Иногда лучше применить Стьюдента (который повысит статистическую мощность), чем отсекать часть результатов и потом ломать голову, как интерпретировать связи изначальных переменных и возиться с повышенным шансом ошибки первого рода.
Более простой вариант: wilcoxon.test с
conf.int = TRUEдля построения доверительных интервалов. Еще проще — бутстрэп.Denis Chernov
Как считать ANOVA ручками?
Цветков Максим
ANOVA позволяет сравнить более двух выборок. Название «дисперсионный анализ» нам намекает, что метод оценивает дисперсию между группами и внутри групп. В каждой группе должно быть нормальное распределение, независимость данных и нужна однородность групп. В ANOVA мы полагаемся на F-test для оценки статистической значимости, от него же и идет p-value. В контексте ANOVA, если F-статистика имеет высокое значение, то как минимум одна группа имеет отличия от остальных. Для понимания, какая именно группа имеет отличия, понадобятся post hoc-тесты. Как было указано в статье, существует One-way ANOVA и Two-way ANOVA.
One-way ANOVA. Это наиболее часто используемая ANOVA, которая может применяться для сравнения средних значений трех или более групп. One-way ANOVA дает общий тест на значимость, но не указывает, какие именно группы отличаются друг от друга. Для одностороннего ANOVA F-статистика представляет собой отношение (межгрупповая дисперсия)/(внутригрупповая дисперсия).
Two-way ANOVA. Это расширение ANOVA, позволяющее анализировать две независимые переменные одновременно. При этом изучаются основные эффекты каждой независимой переменной, а также эффект их взаимодействия на зависимую переменную.
Пример: у нас есть три группы.
System A: {12.5, 10.2, 11.3, 13.1, 11.8}
System B: {9.8, 10.5, 12.1, 11.6, 10.9}
System C: {11.7, 13.2, 12.3, 12.9, 11.5}
Мы формируем гипотезы:
Нулевая гипотеза (H0): нет разницы. Альтернативная гипотеза (Ha): есть разница. Уровень значимости зададим как 0.05 (5%).
Подсчитываем статистику:
Среднее для системы A: meanA = (12.5 + 10.2 + 11.3 + 13.1 + 11.8) / 5 = 11.78.
Среднее для системы B: meanB = (9.8 + 10.5 + 12.1 + 11.6 + 10.9) / 5 = 10.98.
Среднее для системы C: meanC = (11.7 + 13.2 + 12.3 + 12.9 + 11.5) / 5 = 12.32.
И общее meanG = (meanA + meanB + meanC) / 3 = (11.78 + 10.98 + 12.32) / 3 = 11.69.
Далее вычисляем сумму квадратов.
1) Рассчитайте сумму квадратов внутри групп (SSW), дисперсию внутри групп, которая измеряет изменчивость внутри каждой группы.
2) Рассчитайте сумму квадратов между группами (SSB), дисперсию между группами, которая измеряет изменчивость между групповыми средними.
3) Рассчитайте общую сумму квадратов (SST) как сумму SSW и SSB, т.е. SST = SSB+SSW.
4) Вычислить степени свободы для SSW (dfSSW) = (n — k) = 12, где n=15 — общее число наблюдений, а k=3 — число групп.
5) И под конец, подсчитать число степеней свободы для SSB (dfSSB) = (k — 1) = 2.
Далее считаем F-значение.
F-value = (SSB / dfSSB) / (SSW / dfSSW) = 2.61623.Открываем таблицу F-распределений, находим критическое значение с учетом уровня значимости и количества степеней свободы, для нас это 0.11403.
И наконец, мы можем сделать выводы. Поскольку p-значение больше нашего уровня значимости 0,05, мы не можем отвергнуть нулевую гипотезу и, таким образом, делаем вывод об отсутствии (статистически) значимой разницы в среднем времени отклика между системами A, B и C.
Denis Chernov
Во, теперь понял) можно также узнать, что такое степени свободы?
Цветков Максим
На уровне концепции, предположим, что у вас есть доступ к 100 разработчикам из аутсорс-компании. И вам нужно собрать команду из 10. Вы выбрали 1 разработчика, теперь у вас 9 степеней свободы. Другими словами, степени свободы это количество наблюдений, которые могут варьироваться в своих значениях. Но есть нечто фиксированное. Скажем, у нас выборка 2,3,4,5 = 14 / 4 = среднее 3,5. Если мы захотим изменить предложенные изначальные значения, среднее все равно должно оставаться 10.
Но если из генеральной совокупности мы взяли много разных выборок, то у них будут отличаться средние, верно? Так вот, как раз стандартное отклонение и отвечает стандартную ошибку в среднем.