PCA: Снижение размерности данных
Снижение размерности это почти всегда плюс. Модель быстрее учится, меньше переобучения, малозначимые признаки не попадают в модель и не портят качество, сплошная экономия. А если модель очень большая (200+), то любой тимлид потребует PCA+umap и робастенько. Рассматривать будем, как не трудно догадаться, метод главных компонент (principal component analysis, PCA), и все, что вокруг него крутится. PCA это простой и известный способ снижения размерности, используется, когда интерпретируемость не важна и можно построить линейные комбинации. Например, в экономике для объединения кучи индикаторов в один доминирующий. Метод заключается в приближении матрицы признаков матрицей меньшего ранга, так называемое низкоранговое приближение. В данном случае target-переменной нет, признаков много и они плохо интерпретируемы, нехватка данных. Эта ситуация как раз для алгоритма PCA (метод главных компонент).
Для начала посмотрим на другие методы снижения размерности и поймем, почему выбор пал на PCA. Существует много способов снизить размерность данных. Алгоритмы снижения размерности пространства признаков делятся на две группы: отбор признаков (удаление наименее важных) и понижение размерности путем формирования новых признаков на основе старых.
Самым примитивным методом снижения размерности является одномерный отбор признаков, работает на основе корреляции каждого признака с основной переменной с дальнейшим отбором признаков по порогу или по заранее определенному количеству. Другой метод снижения размерности это регуляризация L1 регрессии. Увеличиваем регуляризацию и веса признаков равномерно снижаются, просто понижается значение веса. Доходит до нуля, и веса этих признаков, обнулившись, уходят из модели. Первыми уходят наименее важные. Либо при выполнении алгоритма случайного леса признаки участвуют в разбиении и это характеризует их важность. Одномерные они называются потому, что оценка идет только каждого признака в отдельности, а в жизни группа признаков в целом оказывает влияние. Поэтому метод не популярный.
Давайте на примере: берем количество лайков на дрибле как целевую переменную, и от количества работ будет строиться нелинейная зависимость. Первый шот попадает в отдельную категорию и получает много лайков, далее с увеличением количества и качества шотов лайки пропорционально растут. Но при достижении определенного порога количества шотов и подписчиков, дизайнер уже не получает так столь стремительного роста новых подписчиков и лайков как раньше, так как объем аудитории лимитирован. Более того, могут смениться тренды и внимание аудитории уйдет на других дизайнеров. Линейная модель такое поведени не сможет отследить. Можно использовать нелинейные модели, такие как градиентный бустинг или случайный лес. Любая модель с разветвлениями. Логистическая регрессия это линейный признак, построение гиперплоскости в пространстве.
Надо понимать, что фильтрация признаков по p-value это очень плохой вариант, хоть и любимый новичками. P-value с очень большой натяжкой может положительно сказываться на улучшении целевой метрики, особенно для линейных моделей. Результаты сильно зависят от размера выборки. Очень сильный признак может иметь значимую корреляцию с таргетом на маленькой выборке. Если идти таким путем, то пермутированная важность и проверка отобранных фич на кросс-валидации будут правильным выбором.
Раз метод не идеален, то такой отбор признаков подойдет не всегда, ведь нет гарантии сохранения максимума полезной информации. Второй подход это понижение размерности, мы создаем новые признаки на основе старых. Можно посмотреть в сторону Agglomerative clustering, не плохо объединяет мелкие кластеры в большие. В начале работы каждый объект это отдельный кластер, и потом идет объединение в более крупные кластеры. Либо наоборот, дивизимный алгоритм подразумевает начало работы с одного большого кластера, который будет дробиться на более мелкие.
В том же sklearn есть встроенный feature importance, который позволяет посмотреть, какие признаки были важными. Или многомерное шкалирование, или truncated SVD. Вариантов много.
Посмотрим на не жадный алгоритм, это простой перебор всех сочетаний признаков, дискретно оцениваем качество модели. Формула простая: 2y, где y это число признаков. Допустим, у нас есть признаки: фича 1, 2, 3, 4. Сначала мы оцениваем каждый признак по отдельности, затем начинаем комбинировать все возможные варианты: 1+2, 1+3, 1+4, 2+3, 2+ 4 и так далее. Если у нас всего 4 признака, то алгоритм вполне подходит, так как сохраняет свою эффективность. Но в реальной работе признаков больше, и придется переключиться на жадный алгоритм.
Есть два вида жадных алгоритмов. Мы можем строить модель от одного признака, и выбирать лучший признак, это восходящий вариант жадного алгоритма. Сначала строим модель по каждому признаку, находим лучший, и добавляем к нему второй признак. Это позволяет сократить количество вариантов. Проверили варианты 1,2,3,4, поняли, что вариант 2 лучший, и пробуем все сочетания с ним. Увидели, что 2+3 работает лучше всех, далее пробуем искать третий признак.
Нисходящий вариант жадного алгоритма берет за раз все признаки и исключаем по одному, шаг за шагом. Это более долгий способ, не будем на нем зацикливаться.
И PCA. Принцип метода главных компонент: берем пару признаков, длина и ширина смартфона. Они почти наверняка будут коррелировать. Получаем матрицу ковариаций, оставляет вектора с наибольшими собственными числами. Таким образом можно «сжать» количество признаков в меньшее количество. Понятно, что в продакшене признаков может быть 100, а мы захотим «ужать» их в 50. Или 1000 признаков в 50. Первая компонента забирает большую часть информативности и далее информативность убывает, поэтому не факт, что новые 50 признаков самые сильные. После работы алгоритма получаем простые линейные комбинации изначальных фич с разными весами, компоненты. Они отличаются тем, что не коррелируют между собой, после работы алгоритма мы получаем новые признаки.
В примере говорилось про два признака, но кластеризировать можно и по одному ряду данных. Посмотрите на иллюстрацию ниже, пытливый ум сразу приметит, что user 1 и user 2 похожи друг на друга, а user 3,4,5 явно относятся к другой когорте.
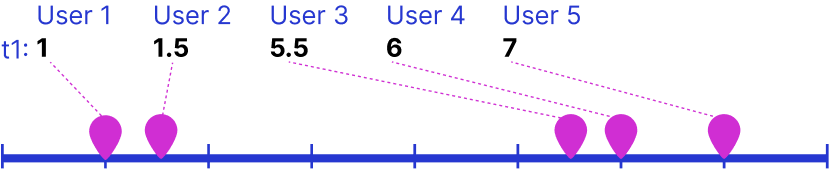
Но при добавлении двух признаков мы должны построить график по двум осям. Опять же, user1 и user2 можно отнести к одному кластеру. При добавлении третьего измерения пришлось бы показывать третье измерение, например размером кружочков на графике. Что уже не так наглядно, а если добавить 4 измерение, то… это уже сложная задача для визуализации. PCA визуализирует быстро, t-SNE модно и может визуализировать даже 4-е измерения. Но дизайнеру придется применять PCA для приведения данных к двум измерениям, так как отчеты начальству требуют простой и понятной визуализации.
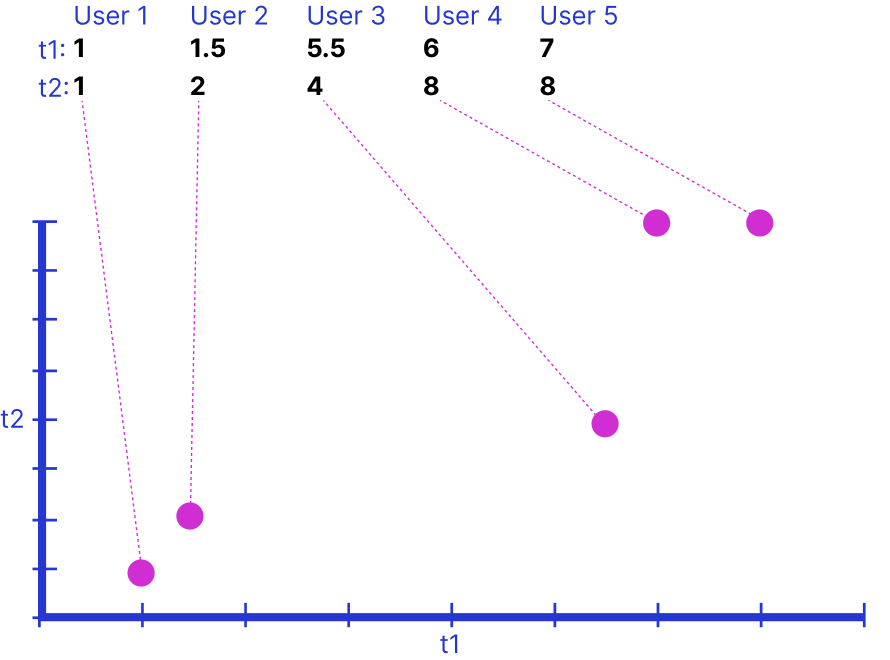
Слева на графике ниже показан принцип «раскидывания» данных по графику, красная точка это среднее, некий общий центр. Он нужен для переноса центра набора данных в центр графика (справа) и поиска такого положения линии, при котором расстояние от всех точек до нарисованной красной линии было бы минимальным. Все это возможно благодаря максимизации суммы квадрата дистанции. Красная линия зовется PC1.
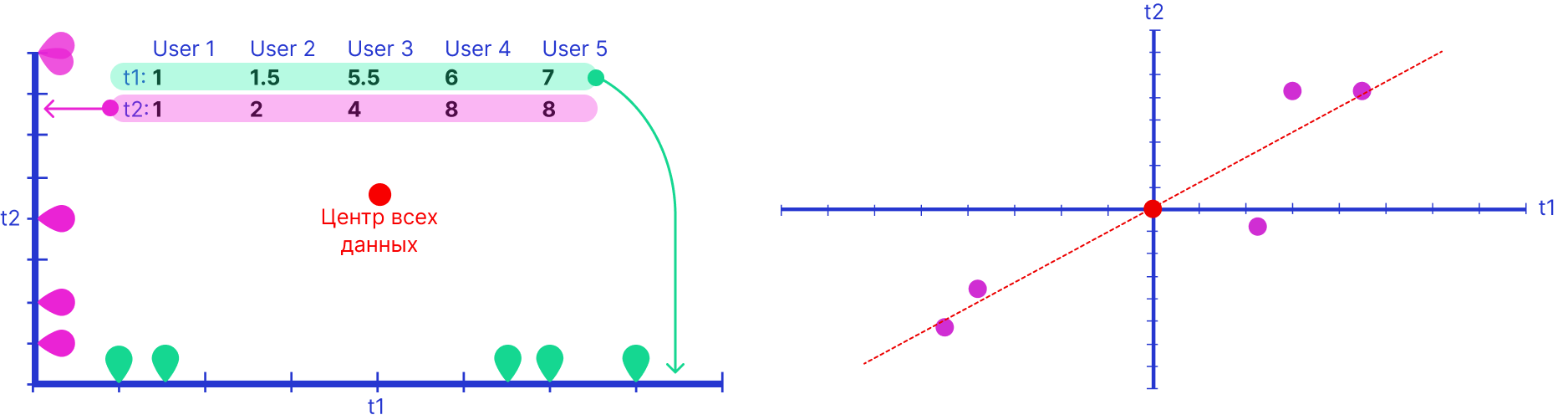
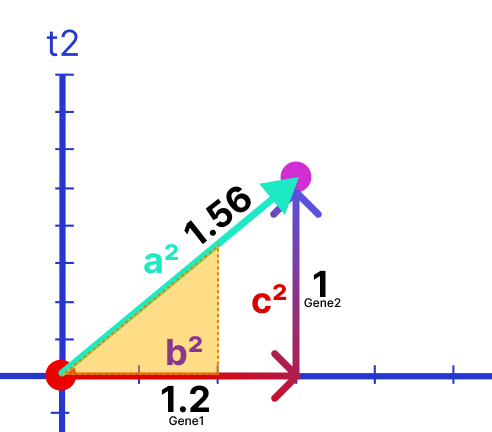
Но как линия строится? Тут мы подходим к ответу на вопрос, почему этот метод называется методом наименьших квадратов. Это просто метод поиска наименьшего расстояния от линии до точки на графике. Расстояние от точки до центра неизменно, мы можем провести красную пунктирную линию А (график ниже). И тут начинается теорема Пифагора: «пифагоровы штаны на все стороны равны», которая используется во всем мире для нахождения расстояний между точками, a2 = c2 + b2 . Идея такая: если с становится больше, то b меньше, и наоборот. Поэтому мы можем использовать либо b, либо с для поиска наименьшего расстояния от точки до линии a. Легче рассчитывать c, минимизируя сумму квадратов расстояний от точек до начала координат. Это делается для каждой точки на графике, значения суммируются, и получаем сумму квадратов расстояний = SS (sum of squares).
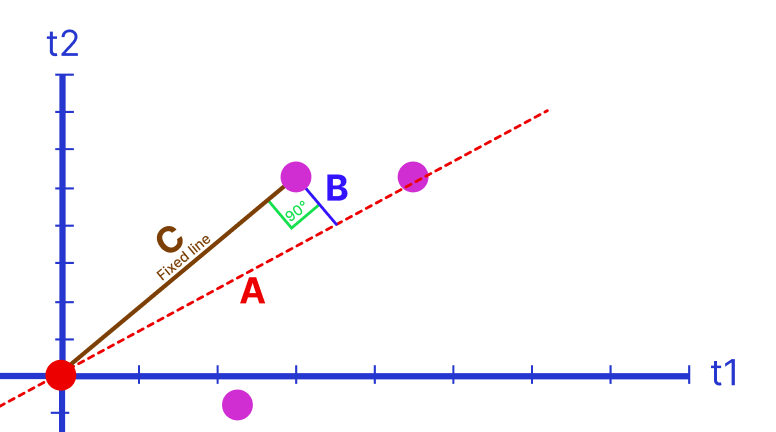
Далее мы вычисляем линейную комбинацию. PC1 это линейная комбинация элементов, формула Пифагора a2 = c2 + b2 , в нашем случае a2 = 1² + 1.2², и возводим в квадратный корень √ . Результат 1,56. Следующий шаг это масштабирование, просто меняем размер полученного треугольника: 1,56 / 1,56 = 1, 1 / 1.56 = 0,64, 1,2 / 1,56 = 0,75. Это наши новые значения, по которым наш треугольник пропорционально уменьшается.
Теорема Пифагора также называется Лемма о перпендикуляре. Для нахождения наилучшего линейного приближения в линейном пространстве для вектора, нужно из вектора опустить перпендикуляр (1 gene2), проекция и будет являться наилучшим линейным приближением. Элемент ŷ это наилучшее линейное приближение Є в линейном пространстве L.
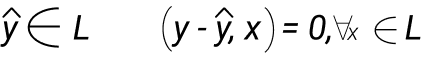
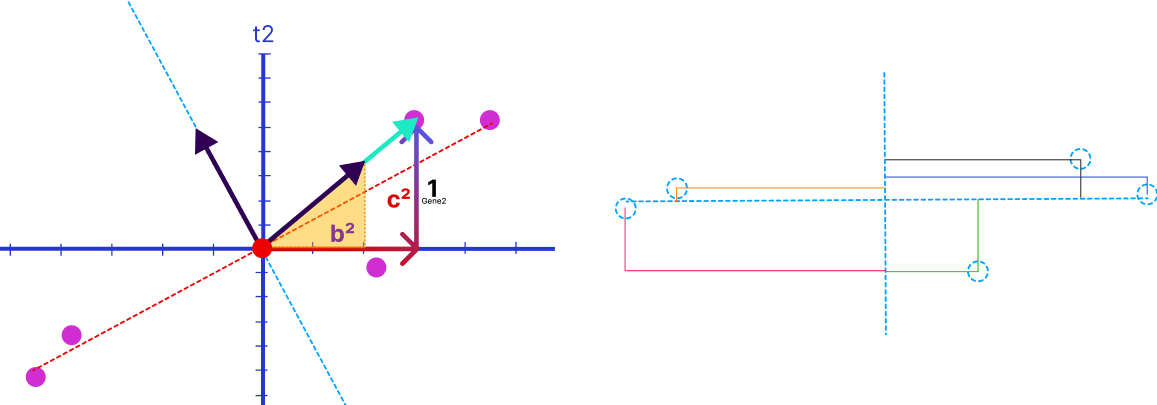
Мы посчитали единичный вектор, это собственный вектор для PC1. С PC1 мы закончили, но еще есть PC2. И это простая перпендикулярная линия к PC1. И, в общем-то, это общая идея, как PCA выполняется с помощью singular value decomposition (SVD). Вы ведь заметили схожесть PCA с сингулярным разложением матриц (SVD)? Метод опорных векторов это аналог сингулярного разложения, но полегче. Из него убрали минимальные собственные значения с соответствующими собственными векторами. думаю, суть понятна: ищем прямую линию, относительно которой наилучшим образом распределяются данные при проецировании.
И тут мы начнем говорить про методы обучения без учителя, или Unsupervised Learning. Именно вместе с ним часто задействован PCA, и кластеризация. Обучение без учителя помогает найти шаблоны в наборе данных. Запоминаем: обучение без учителя это кластеризация. Отсутствует target-переменная, количество кластеров может быть известно. Например, разбросать пользователей мобильного приложения на группы, зная данные о покупках. Или пример алгоритма — k-means. Мы хотим сформировать выборку объектов с признаками, и понять, как они связаны. Мы не ищем точный ответ. Готового ответа не существует, алгоритм попросту раскидывает объекты по кластерам с похожими объектами. Называется это методом k-means, или k-средних. Если бы не он, PCA не был бы так популярен. Простой неконтролируемый алгоритм кластеризации, который группирует признаки по расстоянию между ними. Нагенерим данные:
from sklearn.cluster import KMeans import numpy as np import pandas as pd from sklearn.preprocessing import MinMaxScaler ## все значения от 0 до 1. scaler_0and1 = MinMaxScaler() def generate_dataset(n, seed): shift_matrix = np.array([[1,2], [6,9], [14,2]]) data = np.random.randn(3, 2, n) + shift_matrix.reshape((3, 2, 1)) * 0.101 data = data.reshape((-3, 3)) df = pd.DataFrame({'x': data[:, 1], 'y': data[:, 0]}, columns=['x', 'y']) df = df.astype(float) return df train = generate_dataset(124,432) print(train) |
x y
0 0.237691 -0.378895
1 -0.843438 -1.229108
2 0.732647 -0.513095
3 -0.145382 0.147770
4 -0.010221 0.274869
.. … …
243 1.139096 0.789607
244 -0.407632 0.706096
245 0.580292 0.598956
246 0.260324 -1.176885
247 -1.233812 1.091857Теперь давайте обучим fit_predict и посмотрим, к какому кластеру (будет обозначен цифрами) мы отнесем то или иное наблюдение. Для начала укажем число кластеров, которое хотим получить. За это отвечает параметр n_clusters.
from sklearn.cluster import KMeans train_scaled = scaler_0and1.fit_transform(train) kmeans = KMeans(n_clusters=3, random_state=0) print(kmeans) train_labels = kmeans .fit_predict(train_scaled) print(train_labels) |
[2 2 2 2 0 0 0 0 1 2 0 2 2 2 2 0 2 2 2 2 1 1 2 0 1 2 1 0 2 2 2 2 2 1 2 1 0 2 2 0 0 0 0 0 0 2 0 2 2 0 1 0 1 0 2 2 1 2 0 0 0 1 2 2 1 0 1 2 0 1 1 2 2 0 2 0 2 2 0 0 0 0 1 1 2 1 0 1 2 2 1 0 1 2 1 1 2 2 2 2 0 0 2 2 1 2 1 1 2 1 2 1 2 2 0 1 1 1 1 1 0 0 0 2 0 1 1 1 1 0 1 0 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 0 1 0 0 1 0 0 0 0 1 0 1 1 1 0 1 1 0 1 2 1 0 0 1 1 1 1 1 1 1 0 1 0 0 0 0 0 0 1 0 1 0 0 0 1 1 0 0 1 0 1 2 1 1 0 1 0 2 0 1 2 0 0 2 2 1 0 2 2 2 2 2 2 2 1 2 2 1 2 0 1 1 2 2 0 0 0 1 2 1 2 2 1 0 2 2 1]
Визуализируем в цвете. Допустим, у нас были данные о разном поведении пользователей, они разбились на три кластера. Сначала берем датасет train и визуализируем. Красные ромбы это центры кластеров, так называемые центроиды.
import matplotlib.pyplot as plt centers = scaler_0and1.inverse_transform(kmeans .cluster_centers_) plt.scatter(train['x'], train['y'], c = train_labels) plt.scatter(centers[:, 0], centers[:, 1], marker='D', color = 'red') plt.xlabel('потрачено деньжат') plt.ylabel('просмотрено контента') plt.title('Данные для тренировки модели') |
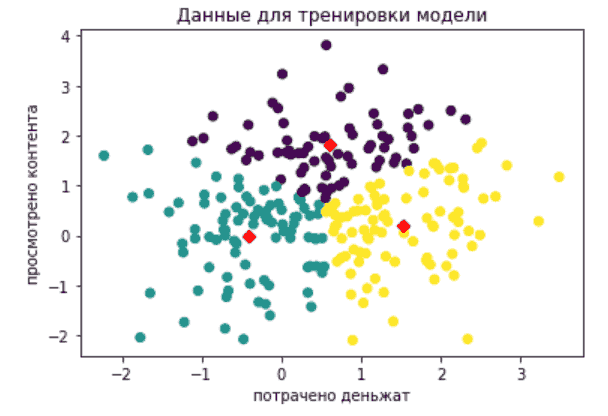
Резонный вопрос: после построения scatterplot может получиться так, что все точки будут равномерно раскиданы и нельзя визуально разделить на кластеры. Тогда можно пробовать докидать фич.
Теперь посмотрим на инершию, то есть на сумму квадратов расстояний от объектов до центров их кластеров. Чем меньше — тем лучше, у нас 8.18320090646764. Если кластеров столько же, сколько объектов, то инершия равна нулю, но нам нужно разумное количество кластеров. Получить инершию просто: print(model.inertia_). Стремимся к балансу между числом нужных нам кластеров и величиной inertia.
test = generate_dataset(443, 563) test_scaled = scaler_0and1.transform(test) test_scaled = pd.DataFrame(test_scaled, columns=['x','y']) test_labels = model.predict(test_scaled) print(test_labels) |
Видим, что центроиды с тестовых данных подходят к основным данным.
И понижение размерности данных: у нас есть датасет с объектами, и мы хотим обучить дерево решений предсказывать целевую переменную. Но у объектов слишком много признаков. И тут нам на выручу приходит PCA (principal component analysis), или метод главных компонент. Вычисляется ковариатационная матрица для данных, а для матрицы вычисляются собственные векторы и значения. В мире продакшена принято делить данные на числовые и категориальные признаки, и каждому отдельно снижать размерность. Заодно будет удобнее настроить интерпретируемость за счет назначения главной компоненте нормального имени.
Для начала приведем все признаки к нужному масштабу, это стандартизация или нормализация. Есть набор данных с двумя признаками: нулевой столбец это диагональ экрана смартфона, первый столбец это количество промазываний по ключевым кнопкам в приложении. Напомню, что наблюдения всегда располагаются в строках, а признаки в столбцах. Если это визуализировать, то видно, что два признака сильно коррелируют.
import numpy as np import matplotlib.pyplot as plt phones = np.array([[5.5, 0.61], [5.1, 0.55], [1.4, 0.21], [3.5, 0.34], [7, 0.81], [6.3, 0.78], [7.2, 0.95]]) plt.scatter(phones[:, 0], phones[:, 1]) |
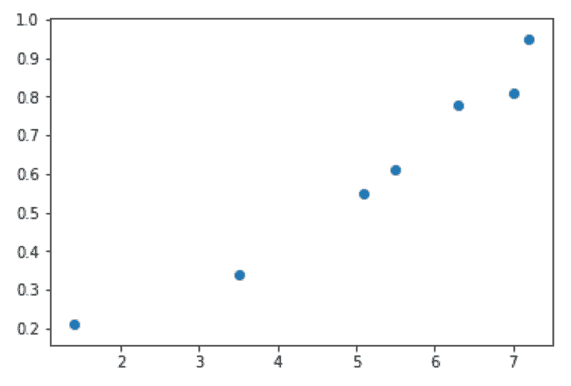
Данные выстроились по прямой линии, значит, можно сжать данные до одного измерения. У нас будет одна главная компонента с минимальной потерей информации.
Следующий шаг это центрирование данных: делается очень просто, mean_values = np.mean(phones, axis=0), потом получаем преобразованное новое значение признаков: phones_centered = phones - mean_values. Теперь среднее каждого признака равно нулю. И находим матрицу ковариаций для центрированных значений признаков: это многомерный аналог дисперсии. По закону линейной алгебры, векторы будет располагать в столбцах. Поэтому столбцы и строки надо поменять местами, получится транспонированная матрица. covariance_matrix = np.cov(phones_centered.T).
Далее ищем собственные векторы матрицы ковариаций: eigenvaluesm, eigenvectors = np.linalg.eig(covariance_matrix). Тут такая проблема, что это матрица, а нам нужен столбец. Есть решение с помощью метода reshape, получится столбец:
result_pre = np.dot(phones_centered, eigenvectors[:, 0]) result = result_pre.reshape(-1, 1) |
array([[ 0.35476857], [-0.04957755], [-3.76326252], [-1.66326203], [ 1.86798318], [ 1.16962746], [ 2.08372289]])
Ура, мы получили главную компоненту. eigenvectors отвечает за направление (например, 90°), а eigenvaluesm это величина дисперсии в заданном направлении. Чем больше значение, тем больше нам это нравится.
from sklearn.decomposition import PCA pca = PCA(n_components=1) mc = pca.fit_transform(phones) mc pca.explained_variance_ratio_ #array([0.99916695]) |
n_components обычно не более 400. В нашем игрушечном случае полученная доля очень близка к единице (0.99916695). То есть мы потеряем очень мало процентов информации. В банках даже потеря 10% информации считается ок. А теперь используем PCA. В рамках моделей классификации алгоритм вычитает из значения признака среднее его значение.
Давайте подберем параметр k для PCA. Ниже будем строить график кумулятивной суммы, и найдем, сколько компонент отвечает за дефолтные PCA energy = 98%. Кумулятивная/совокупная доля объясненной дисперсии это та доля дисперсии, которая объясняется главной компонентой вместе с предыдущими компонентами.
from sklearn.decomposition import PCA from sklearn import datasets import numpy as np import matplotlib.pyplot as plt iris = datasets.load_iris() dataset = iris.data dataset.shape dataset = dataset.astype(float) pca=PCA().fit(dataset) cumulative=np.cumsum(pca.explained_variance_ratio_) plt.step([i for i in range(len(cumulative))],cumulative) plt.show() |
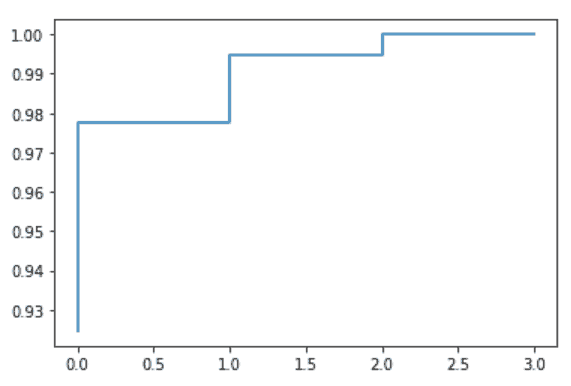
Параметр k для PCA подбирается по «локтю» на scree plot. Принцип простой: на графике по оси X расположены номера главных компонент, а по Y их дисперсии. Где самый сильный сгиб, там и останавливаемся.
pcamodel = PCA(n_components=5) plt.plot(pca.explained_variance_ratio_) plt.xlabel('number of components') plt.ylabel('cumulative explained variance') plt.show() |
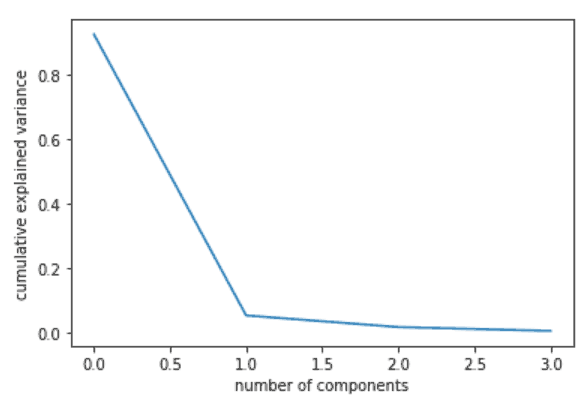
Видно, что цифры нас не обманули, PCA-1 объясняет большую часть дисперсии, чем следующие за ней компоненты. Итак, мы прошлись по цепочке: стандартизация данных -> вычисление ковариационной матрицы -> расчет собственных векторов и собственных значений -> вычисление основных компонентов -> переход от многомерного пространства в двумерному.
Отмечу, что статья про работу с признаками. Для объектов используются другие алгоритмы, например дистилляция данных или SVN, Instance Selection.

6 комментариев
Artyom Burkan
Я так понял, это способ преобразования данных из одного вида к принципиально другому. А как удалить из данных значения по определенному порогу,
Цветков Максим
Если я правильно вас понял, то…. вот набор данных:
И далее удаляем командой
dropвсе те строки, в которых у колонки valid значения меньше 1.inplaceнужен для пересохранения таблицы.Николай Петухов
Максим привет! скажи как можно объединить повторяющиеся элементы разного типа в одно событие?
Цветков Максим
Это разные категориальные данные. Так как нельзя сравнивать числа и объекты, нужно превратить данные в dummy-переменные. тип данных object это, в основном, строковые данные. Колонок станет больше, некоторые колонки пропадут, это называется «оцифровка». Помним, что слишком много признаков = проблемы с обучением моделей.
Либо еще вариант:
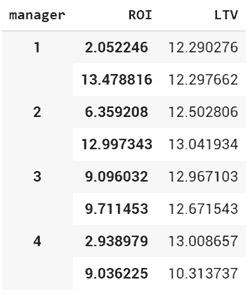
final_df.groupby(['manager','ROI'])[['LTV']].mean()Sasha Zolotarev
Добрый день. Есть результаты опроса, и довольно много. И по опыту где-то 10-15% это мусор. Можно ли отсев мусорных ответов как-то автоматизировать?
Цветков Максим
Взять из статьи метод PCA, уменьшить размерность, потом пройтись DBSCAN. Должен найти кластеры, некоторые из кластеров вполне могут быть мусорными ответами.