Системное мышление в поведенческой экономике
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Люди склонны недооценивать сроки, цепляться за статус-кво. Самый простой способ избежать ошибок это полагаться на проверенные общепринятые правила. Несколько примеров: ограничение скорости на кривых дорогах, пенсионные планы, ипотечные кредиты, готовые варианты выбора страхового полюса, генераторы паролей, гайдлайны дизайн-компонентов. И это работает. Но люди склонны поддаваться искушениям, попадаться на обман, и в общем, мы часто оказываемся в нестандартной ситуации, в которой непонятно, как себя вести. На что опираться, когда нужно принять нестандартное решение? На системное мышление + здравый смысл.
Почему не сработает только системное мышление, спросите вы? Люди одновременно и предсказуемы, и нет. Например, мы неприемлем риск при малой вероятности потерь, но склонны к рискованному поведению, когда вероятность потерь велика. Люди не рациональны по умолчанию, на нас давит недостаток информации, окружение, ограничения временем и собственной ленью. Но при этом рациональность может быть представлена математически, что будет показано ниже.
Если мы не хотим ошибаться, то нам нужно изменить свое поведение и мировоприятие. Изменение поведения человека строится на внешней и внутренней мотивации. Внутренняя мотивация включает возможность влиять на свое поведение, внешняя мотивация про окружение. Какая бы мотивация не использовалась, тратить усилия на постоянное преодоление сложностей весьма накладно по энергии. А окружающий мир постоянно подталкивает нас к определенному выбору, который не всегда нам выгоден. Примеры подходов:
- Фасилитация — уменьшение когнитивных усилий со стороны объекта манипуляции. Например, проставить по умолчанию галочку ‘печатать с двух сторон бумаги’ в настройках принтера. Так мы подтолкнем к уменьшению потребления бумаги. Или наличие чек-листов. Добавление маркеров на еду с рейтингов нутриентов, или предложение заменить вредную еду в корзине на полезную.
- Противостояние. Добавление уровня риска, чтобы люди начали более аккуратно расценивать свой выбор. Например, таймеры на отправку сообщений, наглядные уведомления об потенциальном риске публикации персональных данных или установке с виду безобидного софта. Все уведомления должны соответствовать принципам NEAT: Necessary, Explained, Actionable, Tested.
- Обмануть насчет правды. Сделать картинку определенного товара более привлекательной и сияющей, поднять цену на товар и после этого дать скидку. Плацебо-эффект, искаженная инфографика — все это примеры обмана.
- Социальное влияние. Если официантка подает счет с мятой, жвачкой и антибкатериальной салфеткой, то у нее выше шанс получить чаевые. Или шеринг результатов в социальной сети, рейтинги достижений. Дети становятся более послушными, когда узнают, что совершенные ими действия будут знать родители.
- Страх. Дефицит ресурсов всегда работает. Покупка билетов заранее, запастись консервами, купить лимитированную футболку. Также, пережитые проблемы ведут к изменению покупательского поведения: если вы пережили наводнение, то почти наверняка будете покупать страховку от наводнения.
- Усиление. Например, усиление тряски машины, если водитель разгоняется слишком сильно.
Из этого можно сделать вывод, что одинаковая проблема может по разному восприниматься, если она представлена по разному. Поэтому важно стремиться к консистентности в своих решениях.
Свои особенности накладывают разные культуры. У всех есть некие стереотипы относительно поведения людей из разных стран. Скажем, немцы — пунктуальные, а шотландцы — патриотичны. И это правда, люди из разных стран воспринимают мир по разному. Если в Беларуси принято ходить в лес за грибами и это норма, то для бразильцев это звучит диковато. Отличия в культуре можно структурировать:
- Дистанция между участниками в плане власти
- Отношение к неопределенности
- Индивидуализм против коллективизма
- Маскулинность против женственности. Маскулинность про соперничество
- Приоритет на долгосрочные ценности или короткие этапы. Исторически, люди ценят либо традиции, либо изменения
- Беззаботность жизни или стабильность семьи
Подумайте про свои приоритеты исходя из пунктов выше. Это ваша опора при принятии решения для себя. Либо применить подход Майера, что больше подходит для корпораций:
- Общение — простое, высокоуровневое, понятное, неформальное, или коммуникация вовлекает много сложных деталей?
- Оценка — прямой негативный фидбек или мягкие методы подачи обратной связи?
- Лидерство — эгалитарное или иерархическое?
- Доверие — основано на задачах, или без темной коллаборации и неформальных знакомств контакта не будет?
- Принятие решений — сверху вниз или консенсус команды?
- Степень толерантности к несогласию с решениями коллег и руководителей?
- Планирование — быть гибким или строго придерживаться планов?
- Убеждение — дедуктивные методы (германские и восточноевропейская) или индуктивная логика?
Все это сильно влияет на внутреннюю и внешнюю мотивации. Нужно понимать свою роль в конкретном окружении и исходя из этого не позволять манипуляциям влиять на ваши решения.
Бывают очень умные люди, но им не даются системные дисциплины. Например, они не могут нормально сделать mind-map. Такие люди мыслят не системно, но интуитивно. Те самые люди, у которых постоянно возникают озарения и инсайты. Но системность позволяет принимать правильные решения на каждодневной основе, и что самое важное, минимизировать ошибки. Если задача включает в себя цифры, то такие люди начинают бояться, что придется решать уравнения. Но уравнения нужны не всегда. Многие задачи очень примитивные, и их можно решить простой формулой. Пример: яблоко стоит $2, а тарелка $4, сколько стоит тарелка с яблоком? Тут не нужно уравнение, легко считается в уме. Или у нас есть 30 красных, 40 белых и 30 черный монеток в коробке. Какова вероятность достать красную монетку? Если суммарно монеток 100, а красных 30, то шанс 30/100 = 30%.
Задачу можно усложнить: тарелка с яблоком стоит $6, а тарелка дороже яблока на $2. Тоже простая задача, но не торопитесь с выводами, здесь нужно подумать. Другими словами, у нас есть уравнение, где x + (x + 2) = 6, или 🍎 + (🍎 + $2) = $6 и как только мы представили формулу визуально, ответ также стал нагляднее. 2x = 6 — 2, и 2x = 4 / 2 = 2. Простое линейное уравнение.
Другой пример с системой уравнений. Орех в сиропе стоит $240, и сироп дороже ореха на $80. Это можно представить как:
- орех + сироп = 240
- сироп — орех = 80
- Решаем методом подстановки:
- орех + (80 + орех) = 240
- 2орех = 240 — 80
- 2орех = 160
- орех = 80
Вернемся к задаче с цветными монетками, но слегка ее усложним. По прежнему имеется 30 красных, 40 белых и 30 черный монеток в коробке, но в этот раз сначала извлекается одна монетка, кладется на место и извлекается вторая. Какова вероятность извлечения белой и черной монетки? Казалось бы, это сложная задача: события зависимые или независимые? Начнем рассуждать. P (вероятность синего * вероятность зеленого). По факту нам не важно, когда монетки достали, нас лишь важно вероятность, что в руках побывает белая и черная монетки. Вероятность для белой монетки 40/100, для черной 30/100. И находим произведение вероятности, которое в виде формулы P(AB) = P(A) ∙ P(B). По факту, это просто 0,4 * 0,3 = 0,12.
Вероятность встречи
Сложные решения в жизни всегда про вероятность. Мы не можем быть уверены в результате исхода событий, но нужно принимать решения. Вероятностные события лучше оценивать математически, а не умозрительно. Например, два человека договорились встретиться в определённом месте между 10 и 11 часами. Пришедший первым ждёт другого 20 минут, после чего уходит. Чему равна вероятность встречи, если каждый из них может прийти наудачу независимо от другого в течение указанного часа?
Стараемся вытащить из задачи все числовые значения. У нас есть 60 минут как диапазон между 10 и 11 часами. Время прихода первого человека x-t1, время прихода второго x-y2. Так, |x-y| ≤ 20, и значение должно быть точно положительным. Такое выражение можно выразить системно, раскрыв модуль:y ≥ x - 20y ≤ x - 20

Полученные уравнения мы можем представить визуально на графике, в котором учтено, что время может быть только положительным (оси x,y от 0 до 60). Синие квадратики говорят нам о том ,что треугольнички прямоугольные, и их площадь считается как 1/2 на произведение катетов. Тогда они равны 60-20 = 40. Значит:
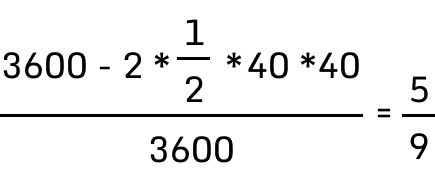
При площади всего квадрата 3600, вероятность встречи 5/9. Сверху можно накинуть культурные особенности, например, арабы персидского залива и испанцы склонны опаздывать. И так степень уверенности в принятии решения относительно встречи значимо возрастает.
Подбрасывание монетки
Алгоритм Монте-Карло ассоциирован с моделированием подбрасывания монеты. Математически, генерируется псевдо-случайное число от 0 до 1, и если будет сгенерировано число в диапазоне 0-0.5, то орел, решкой будет считаться значение в диапазоне 0.5-1. Для реализации такой логики используется относительная частота появления случайного события W (A) = m/n, где m — число появлений события А, n — общее кол-во испытаний. Данный пример характеризует несовместные события, т.е. не может одновременно выпасть и орел, и решка. Выпадение орла это невыпадение решки. Выпадение орла или решки являются зависимыми событиями, другими словами, появление одного события влияет на вероятность появления другого события. Также, это является достоверным событием, такое событие обязательно произойдет при определенной совокупности условий.
А вот кол-по подбросов монетки это уже независимые события. Даже если выпал 50 раз подряд орел, это не увеличивает шанс выпадения решки во время следующего подбрасывания.
В теории вероятности, если события A и B несовместимы, тогда P(A+B) = P(A) + P(B). Если A,B несовместимые события, то сумма их вероятности будет P(A) + P(B) =1. 0.5 + 0.5 = 1. Если A и B зависимы, то вероятность наступления обоих событий выражается произведением P(AB) = P(A)*P(B/A). Это можно представить в виде кода:
import numpy as np s = np.random.uniform(1,0,20) print(s) |
import numpy as np for i in range(0,5): a = input() x = np.random.uniform(0,10) if x<5: print('орел') else: print('решка') |
Бросание кубиков
Бросают две игральные кости. Какова вероятность, что сумма очков меньше или равна 5? Такого рода задачки решаются по формуле n/N, где n это кол-во благоприятных исходов, и N — все возможные варианты. Рисуем табличку, в заголовок которой выписываем потенциальные результаты 1,2,3,4 для первой кости. Мы не выписываем 5 и 6, так как это не является благоприятным исходом события. Все остальные строки это потенциальные благоприятные исходы для второй кости при условии, что первая кость выдала значение из заголовка таблицы.
| 1 | 2 | 3 | 4 |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | |
| 3 | 3 | ||
| 4 |
Так мы находим n = 10, и N = 36 (6*6). P = 10/36 = 0,27 является ответом.
Аналогично можно решить задачу с картами. Какова вероятность извлечения дамы или короля из колоды в 36 карт? Это несовместимые события (или), значит используем теорему сложения P (A + B) = P (A) + P (B). P (Дама + Король). Классическое определение вероятности P = n (благоприятные исходы)/N (все варианты). Так как в колоде 4 дамы, P = 4/36. Аналогично для кородя, 4/36. Получаем 4/36 + 4/36 = 8/36.
Разорение фирмы
Фирма участвует в 4-х проектах, каждый из которых может окончиться неудачей с вероятностью 0,1. В случае неудачи в одном проекте, вероятность разорения фирмы равна 20%, двух – 50%, трёх – 70%, четырёх – 90%. Определите вероятность разорения фирмы.
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна P, событие наступит ровно K раз, вычисляется по формуле Бернулли. Где q — вероятность противоположного события, q = 1-p (событие). Формула Бернулли:
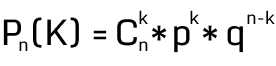
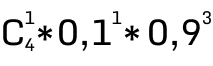
0,2, если первый проект будет провален. Подсчитав вероятности по всем 4 проектам, мы можем подсчитать общую вероятность, P = 0,29160,2+0,04860,5+0,00360,7+0,00010,9=0,0860Дискриминант
Простое квадратное уравнение: x²-3=0, надо найти x. x² = 3, значит x= +- √3.
Чуть более сложное квадратное уравнение, a * x² + b * x + c = 0, решается через дискриминант (то, что под знаком корня). Формула будет следующей:
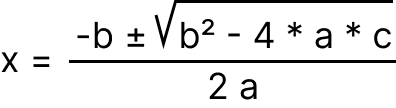
Подставим значения в квадратное уравнение: 2 * x² + 7 * x - 1 = 0. В дискриминанте 2x2+7x-1, что пересчитывается в D=72 - 4·2·(-1)=57.
Усложняем, переходя на дробно-рациональные уравнения. Освежаем школьную программу: знаменатель не может быть равен нулю, потому что мы не можем делить на ноль, по крайней мере в рациональных уравнениях. Первый шаг решения таких уравнений это попытка найти ОДЗ (x), то есть те значения, которые в данном уравнении мы не сможем получить. И тогда мы сможем найти нужные значения.
В примере ниже x ≠ 0, и x ≠ 3. Следующий шаг это приравнивание к общему знаменателю. Общий знаменатель это комбинация из всех знаменателей, в ниже примере это 3-x и 2 и x(3-x), которые будут представлены как общий знаминатель 2x(3-x).
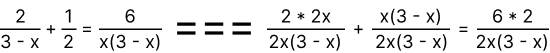
Помним, мы домножаем на то значение, на которое делили. Получаем квадратное уравнение 4x + 3x - x2 = 12. И x2 - 7x + 12 = 0. И тут вернемся к теме дискриминанта, чья формула D = b2 - 4ac. Находим корни: x₁ = -(-7) + 1 / 2 = 4, и x₂ = -(-7) - 1 / 2 = 3. Как видим, одна и таже переменная имеет два разных значения. Мы получили совопупность.

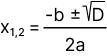
Парадокс Монти Холла
Есть три двери: за двумя дверьми скрываются козы, за одной — машина. Цель игры — найти машину. Игрок должен выбрать одну дверь, после чего ведущий откроет любую другую дверь, за которой сидит коза. И игрок имеет право сменить решение и выбрать другую дверь. Такого рода задачка решается, опять же, табличкой:
| Автомобиль | Выбор игрока | Победа без изменения выбора | Победа с изменением выбора |
|---|---|---|---|
| Дверь 1 | 1 | 1 | 0 |
| 2 | 0 | 1 | |
| 3 | 0 | 1 | |
| Дверь 2 | 1 | 0 | 1 |
| 2 | 1 | 0 | |
| 3 | 0 | 1 | |
| Дверь 3 | 1 | 0 | 1 |
| 2 | 0 | 1 | |
| 3 | 1 | 0 |
3/9 или 6/9 — где больше шансов, весьма очевидно. Такого рода лотерея говорит нам о том, что если часто менять выбор, то больше шансов победить.
Линейная алгебра.
Раз мы так любим таблицы, то давайте поглубже затронем тему матриц. Матрица это таблица, в которой есть элементы в строках и столбцах. И с такой матрицей мы можем выполнять определенные операции. Условно, одна колонка или строка это вектор, который с точки зрения линейной алгебры является упорядоченной последовательностью цифр. Вектор с размерностью одна единица это попросту одно число [x₁]. Модуль вектора это его длина.
Рассмотрим простой вектор x = [10,2]. Катеты будут составлять x₁ и x₂, и гипотенуза. По теореме Пифагора, сумма квадратов катетов равняется квадрату гипотенузы: две синие стрелки в сумме дают фиолетовую. Ниже представлены два вектора синего цвета, и вектор x будет складываться по правилу треугольника. 10²+2² под корнем это 100 + 4 = √104 = 10.1980.
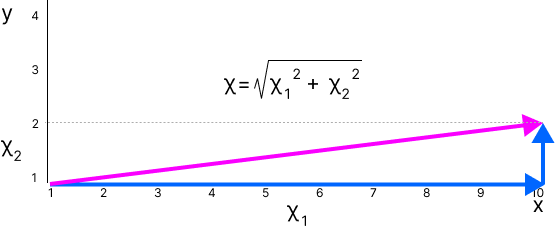
В 3D-пространстве вектор определяется тремя координатами. Так, вектор x = [x₁ x₂ x₃], три координаты. Длина аналогично вычисляется как корень квадратный из суммы квадратов координат. Это позволяет рассчитать расстояние по прямой, или длину линии между точками.
Уравнение плоскости в отрезкахAx + By + C*z + D = 0. В примере ниже, если y и z = 0, то точка плоскости пересекает ось x в точке по формулам ниже.

Другое упражнение.(5E)^(-1), где -1 не степень, а показатель обратной матрицы. Другими словами, нам нужно найти обратную матрицу к 5E. Python может выдать какой-то результат, но правильный ответ — нет решения. Мы не можем из матрицы вычесть число. Но если преобразовать -1 в матрицу из множества единиц, тогда уравнение решаемо.
Обратная матрица это матрица, которая при умножении на свою нормальную матрицу дает E. A * A-¹ = E. Тогда, обратная матрица (1/3*E)^(-1) = 3E, так как матрица 3E * (1/3 * E) -¹ = E.
Другой пример, у нас есть матрица, и мы хотим подсчитать по правилу Саррюса определитель.
1 2 3
4 0 6
7 8 9Мы берем первые два столбика из оригинальной матрицы (синие столбики 4 и 5), и по диагонали считаем определитель:
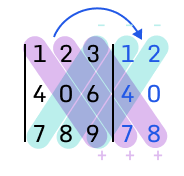
Перемножаем и складываем все главные диагонали: 1 * 0 * 9 + 2 * 6 * 7 + 3 * 4 * 8. второстепенные диаганали: 84 + 96 - 48 - 72 = 60, это и есть определель. Такой метод применяется только к матрицам 3×3.
Логарифм
Определение логарифма. Решение уравнения:
2**x = 300
x = log₂ (4 * 3 * 5²)
x = 2 + log₂ 3 + 21 log₂ 5
x = in 300 / in 2
x ≈ 8.23Норма вектора
Манхэттенское расстояние и Евклидова норма, они же L1 и L2. Используется для поиска пути из точки А в точку B. Раз у нас две точки, то напомню, что геометрическое расстояние между точками измеряется по теореме Пифагора.
Манхэттенское расстояние это сумма каждого элемента из вектора X. Находим длину, по которой можно пройти разными способами. Евклидово расстояние тоже про поиск пути из точки А в точку Б, но условие — ищем самый быстрый маршрут.
Начнем считать. Нам нужно определить норму вектора для начала и конца маршрута, где a = (1,2,3) и b = (-1,-1,0). Как первый шаг, транспонируем матрицы, вычитаем координаты конца из координат начала и получаем координаты вектора ab:(-1 -1) = -2
(-1 -2) = -3
(0 - 3) = -3
Далее применяем две формулы для Манхэттенского расстояния и Евклидова расстояния:
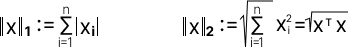
|| AB ||₁ = |-2|+|-3|+|-3| = 2 + 3 + 3 = 8 и || AB ||₂ = √(-2)² + (-3)² + (-3)² = √ 4+ 9 + 9 = √ 22. Евклидова расстояние включено в норму вектора.
Геометрическая вероятность
В квадрат вписан круг. Нас интересует, с какой вероятностью случайная точка попадет в круг. В условии задачи нет ни одного числа, есть просто квадрат и круг.
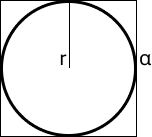
Начнем рассуждать, что для нас благоприятный исход? Попадание в круг, берем это как n. Площадь квадрата как все возможные исходы равны N. Формула будет уже знакомая n/N.
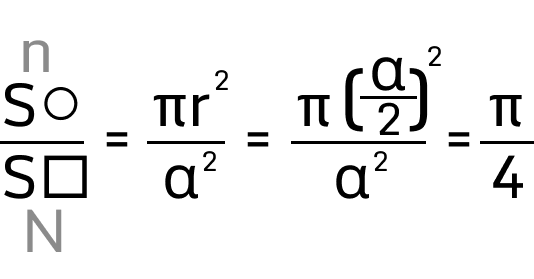
Такие упражнения помогут сформировать системное мышление и далее, перейти к холистическому мышлению. А критическое мышление уже должно быть.

2 комментария
Виктор
Привет! хочу начать работать на себя и создать айтишный продукт. вычитал блок, понял что нам надо создать МВП и его кастдевить на клиентов. Это реально так работает?) какой процент успеха?
Цветков Максим
Выживает очень мало стартапов. В формуле «клиент > проблема > решение через ценность» нужен множитель в виде нечестного преимущества. Не надо общаться с клиентом слишком рано. Сейчас все ЛПРы уже устали от бесконечных кастдевов и попыток найти их очередную боль.
У вас должен быть доступ к базе клиентов. Если нету базы клиентов, то и некому продавать. Например, у вас есть пет-проект с симуляцией питчинга проектов, и им пользуется 2 000 людей в месяц. Это ваша база, вам надо собрать их почты/телефоны/что угодно и аутричить их релевантным платным продуктом, вокруг которого строится монетизация вашего бизнеса. Нету базы — идите на конференцию и собирайте список участников, это ваша база. Далее, создаете аккаунты LinkedIn, через GetSales делаете рассылки, и устраиваете аккаунты в компанию в LI. Для рассылки с почты, нужны почтовые ящики, к примеру 1 ящик на гугле может рассылать около 200 писем в день. Их можно нагенерить через Maildoso, чтобы не портить репутацию домена рассылками. Добавляете адреса в snov.io и запускаете рассылку.
Когда достучались до клиента, отправляете им опросник, даете промо-код на MVP, с наиболее активными проводите интервью. Пробуете продать им уже работающий MVP или прототип. Представляетесь фаундером и строите отношения, а не играете в менеджера по продажам.