Математика в геймификации
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Хорошая игра, как и любой хороший продукт, характеризуется грамотным балансом и воспроизводимым успехом. Нет воспроизводимости = магия. Технически, это всем известное CPI < LTV. Но когда мы занимаемся прелиминарной балансировкой, то никуда не уйти от retention day 1, day 3 и прочих метрик. Посмотрим на простую задачу: на игровом уровне за 5 минут при 3 сессиях в день игрок делает 30 тапов, каждый тап дает 1 единицу золота. 5 * 3 * 30 * 1 = 450 золота в день, на которые игрок может приобрести нужное количество контента. Но это один игрок, который играет каждый день, а другие игроки заходят раз в неделю. У некоторых в таком случае будет меньше денег/редких предметов, у других больше. И многие игроки перестанут получать поток удовольствия от игры и монетизация не будет приносить доход. Давайте сгладим пропасть между богатыми и бедными. На входе можно давать +50 золотых, на первые 20 тапов давать x2 золота, а после 80 тапов каждый второй тап дает x0,5 золота. Это сократит финансовый разрыв между игроками. О таких простых, но эффективных способах работы с геймификацией мы и поговорим в этой статье.
Геймификация — это не про рейтинги и звания за достижения, а про мотивацию. Октализ.
Инфляция может быть не только финансовая, но и инфляция интереса. Игроку с высоким уровнем прокачки становится все менее интересно играть в игру, нам нужно его достижения и опыт немного девальвировать. Играя в Lineage 2 десять лет назад, люди тратили годы на прокачку персонажа, сейчас же можно прокачаться до высоких уровней за пару недель. Это осознанный шаг авторов, слегка девальвировать превосходство опытных игроков, а новым игрокам позволить быстро догнать старичков. Для реализации такого используется простая геометрическая прогрессия, где предыдущий опыт домножается на некий коэффициент и выдается новым участникам. Существуют разные виды прогрессий, давайте разберем самые популярные. Можно сверху докинуть эффект значительного прогресса.
Итак, новый игрок начинает игру голым персонажем, и в состоянии убить одного монстра. Убив несколько монстров, он получает достаточно золота для покупки самых простых брони и меча. И далее замкнутый круг, убивает более сильных монстров, покупает более крутые предметы, убивает еще более крутых монстров и так далее. Такое развитие можно реализовать самой обычной прогрессией +10%, а можно сделать интереснее, использовав числа Фибоначчи + модификатор 0,75%.
Фибоначчи это последовательность чисел, в которой каждое новое значение равно сумме двух предыдущих (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144). Не так быстро растет, как геометрическая прогрессия, что дает больше шагов роста игроку.
Ниже представлена упрощенная версия доски Гальтона. Цифры внутри шестигранника это шанс, с которым событие может произойти в данной ячейке. Чем ближе к центру, тем больше вероятность события, так формируется нормальное распределение данных. Но если провести линии от каждой цифры вдоль шестигранника, то мы также получим идеальную последовательность 0, 1, 1, 2, 3, 5, 8, 13.
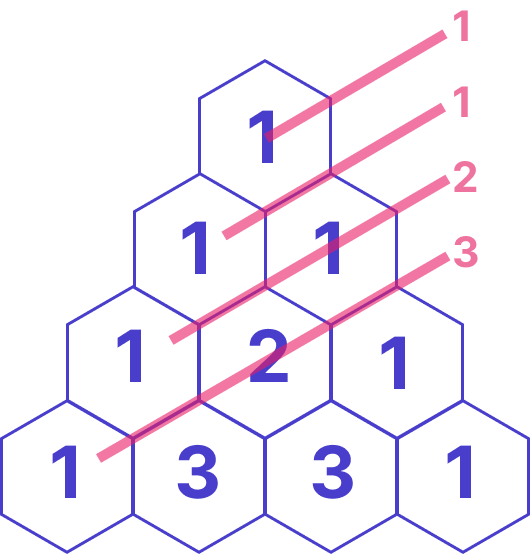
В арифметической прогрессии каждое новое значение, начиная со второго, равно предыдущему, сложенному с постоянным для этой последовательности числом d. Число d называется разностью прогрессии (0,2,4,6,8,10 d=2). По началу растет быстро, но с каждым новом шагом все больше отстаем по величине значений от рядов Фибанначи и геометрической прогрессии. Да и высчитать арифметическую прогрессию игрокам слишком просто.
В геометрической прогрессии каждое последующее число, начиная со второго, получается из предыдущего умножением его на определенное число q — знаменатель прогрессии. (1,3,9,27, при q = 3).
Почему мы делаем начало игры легким? Вопрос простой, в начале игрок учится, далее, с ростом скила, прогресс идет сложнее и медленнее. Для усложнения можно использовать и логарифм, и гиперболу, и степенные степени ниже 1. Мы создаем сложность, а игрок готов платить деньги за упрощение игрового процесса и экономию его времени. Так называемые Paywall. Но надо следить за собой и не скатываться в Pay to Win. Всему этому легко учиться, если делать деконстракт механики игр.
Зачем побеждать?
Так как люди играют с другими людьми, то они в большинстве случаев хотят быть лучше среднего игрока. Это ключевая идея геймификации — позитивная обратная связь на действия игрока. Для этого хорошо подходят рейтинги игроков. Рейтинги про то, как люди друг с другом взаимодействуют, или легкий способ как группе людей привить интерес к игре друг с другом. Но это не такая простая задача, как кажется, сортировать игроков можно по силе, по количеству побед, по количеству боев, по баллам за победы. Один из способов выявить сильных игроков и сравнить их это турниры. Они ограничены во времени, и самый логичный вариант провести турнир по круговой системе. Каждый участник играет с каждым по 1 разу, но если у нас 50 участников, то 50*49 / 2 = 1225 матчей. Слишком много, поэтому разберем другие системы.
Олимпийсая система (single elimination), игра на выбывание. Игроки случайным образом сталкиваются друг с другом, победитель остается, проигравший исключается. Формула простая, n-1. Но должно быть четное число участников. И на выходе только победители, остальные просто проигравшие на определенном этапе.
Швейцарская система, игрок играет с близким по уровню игроком. Игроки отсортированы по некому критерию, и с каждым матчем рейтинг переранжируется с учетом заработанных очков. Считать просто, 300 участников и 20 туров, 300 * 20 / 2 = 3000 матчей.
Double elimination — некая вариация олимпийской системы, турнирная система с выбыванием после двух поражений. Отличие в том, что игрокам дается два шанса, а не один, как в single elimination. Проигравший игрок переходит к группу проигравших и играет с другими проигравшими, 2*n — 1. Есть шанс, что игроки встретятся друг с другом дважды. Это система активно используется для киберспорта.
У перечисленных систем есть одно слабое место. Ничья. Это решается увеличением ценности победы, или переходом к другой игре, например, переход к серии пинальти в футболе. В швейцарской системе распространен коэффициент Бухгольца. Если у игроков одинаковое количество очков, то смотрят на тех, у кого выйграли претенденты на призовое место. И по сумме мест определяют, какой игрок пришел к лидерству, соревнуясь со слабыми соперниками. Есть вариация под названием «коэффициент Бергера». И коэффициент Солкоффа, в котором также суммируются очки соперников, но исключают самого слабого и сильного.
На рейтинг могут влиять не только объективные, но и индивидуальные показатели. Поэтому важно сопоставлять игроков с одинаковым качеством соединения, одинаковым скиллом, одиночек или крепкие команды. Рассмотрим способ такого расчета на примере формул рейтинга Эло для двух игроков (изначально разработана для шахмат):

Первый этапД вычисляем шансы на победу игрока А над игроком Б. Вторая формула чуть ниже, в ней мы берем новый и старый рейтинг игрока А, Sα это результат матча, 0 при поражении, 0,5 при ничье и 1 при победе. Eα — ранее вычисленный шанс игрока А на победу. K (key factor), некий регулирующий коэффициента для регулирования скорости изменения рейтинга, по началу он большой, 90-100. При таком значении прогресс в начале игры будет очень быстрый, а в дальнейшем идет снижение коэффициента до 5-10. Как дополнительный плюс, по рейтингу Эло очень легко анализировать информацию, так как данные будут нормально распределены. Есть много способов подсчитать правильное место игрока в рейтингах, помимо рейтинга Эло, еще и теория аукционов, и экономическая теория.

Для сравнения команд потребуется вычислять значения для командного рейтинга. Подойдет система TrueSkill от Microsoft, где стартовый скилл в виде нормального стандартного распределения N, характеризуемого средним значением Mu, и дисперсией sigma.
Итак, как делать рейтинг победителей—понятно. Это очень хороший инструмент для увеличения конкуренции среди игроков, как и киберспорт, тоже просто инструмент для увеличения конкурентности в игровой среде. Рейтинги это самая частотная социальная функция, для Microsoft Xbox Live наличие нейтинга (Leaderboard) это обязательное требование. Работает даже в сингплеере. Leaderboard’ы в первую очередь аффектят ачиверов и киллеров (а это самая большая группа игроков), они хотят больше всего быть лидерами чартов.
А теперь про нюансы. Игрок чувствует себя классным и выше среднего, если у него есть чувство близости к тем людям, с которыми он соревнуется. Необходимо постоянно поддерживать это видение, что игрок либо уже является, либо неустанно идет к цели быть лучше среднего. Несколько примеров: соответствие стандартам навыка, когда игроку падает уведомление, что в плане прогресса навыка «призыв питомцев» он входит в топ 50% всех игроков, и держите за это 20 золота. Надо не просто сообщать, но и награждать. Социальное вознаграждение очень важно, на лайках были построены тысячи успешных сервисов. Когда игра обрастет огромной аудиторией, один большой leaderboard придется разделить на множество маленьких, по уровням, чемпион среди друзей, лучший на сервере, лучший за день в городе, самый сильный танк недели и так далее.
Теория вероятностей
Казино это имитация выбора. Любой игрок хочет оказывать влияние на происходящее в мире. Для этого в игры добавляют разные варианты концовок, разные последствия выбора, сделанного игроком. Это история про комбинаторику, распределения вероятностей и математическую статистику.
Математическая статистика помогает принимать решения. В любой профессии для IT важно знать теорию вероятностей и математическую статистику. Теорея вероятностей учит нас учитывать вероятность, что некое событие случится. Классика: кидаем игральный кубик, и знаем вероятность выпадения каждой из 6-и сторон, у нас есть 100% данных. В статистике нет полных данных, мы работаем с выборками. И важно понимать, никакие математические модели не дадут полного представления о боевом балансе и покрывают собой только простые задачи, но они помогают сильно уменьшить неопределенность.
Введем несколько понятий. Случайная величина — величина (число), которая в результате опыта/эксперимента принимает некоторое значение, неизвестное заранее. Примеры таких величин это температура в городе, количество шагов.
Принято различать как минимум две сущности: дискретные случайные величины принимают конечное или счётное множество значений (например, натуральные или рациональные числа). Это может быть количество чего то, некие целое число. Или сумма очков при множесвенном подбрасывании игрального кубика. Число людей, которые проголосовали на выборах. Количество людей, которые приходят в ТЦ в выходной день. Второй тип, непрерывные случайные величины, принимают несчётное множество значений (например, вещественные числа). В случае с ростом человека, рост 180-181, и не может быть 180,4.
Все это хорошо масштабируется на типы метрик. Либо доли (бинарные 1/0, да/нет), либо непрерывные (время в сек, мин, деньги), либо отношения (кол-во кликов за сессию, цена за 1 000 показов), отношения между двумя случайными величинами. Непрерывные значения и метрики отношений всегда самые сложные для работы. Непрерывные метрики это финансы, ARPV, например чеки в магазине варьируются от 100 рублей до нескольких миллионов, что ведет к сложному распределению и большой дисперсии. Метрика отношений это CTR (пользователи, просмотры, клики), почти всегда системы аналитики находят CTR по каждому пользователю и потом его усредняют, забывая, что у разных значений есть своя дисперсия.
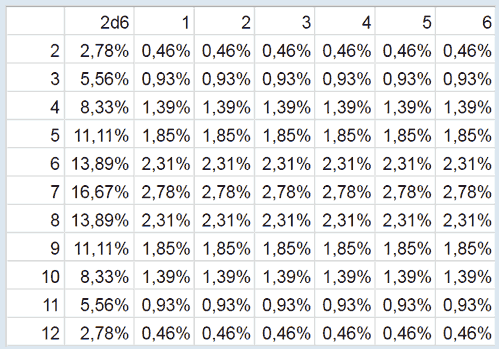
Мы поговорим про дискретные величины. Пусть X — дискретная случайная величина, как и любое число в компьютере. Закон распределения этой случайной величины — это соответствие между значениями, которые принимает эта величина, и вероятностями, с которыми она их принимает. Например, у нас есть два игральных кубика. При одном броске возможные результаты от 2 до 12. Число возможных исходов 36, 6 на одном кубике * 6 на втором кубике. При этом исход 2+1 или 1+2 дадут одинаковый результат 3. Для результата 4 уже больше комбинаций: 1+3, 2+2, 3+1. И так число комбинаций растет до числа 7, семерку можно получить комбинациями: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1. Восьмерка же идет с меньшим количеством комбинаций, так как если у одного кубика выпадет 1, то 8 уже не будет. Это пример определения вероятности каждого значения. Отметим, что сумма вероятностей дискретной случайной величины всегда равна 1, одно из этих значений всегда будет принято.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
Для двух кубиков все расписано просто и понятно. А для трех кубиков можно переиспользовать результат одного кубика с определенной вероятностью. Если построить график распределения вероятностей для двух или трех кубиков, то в обоих случаях будет колокообразная история. Но! очень важно обратить внимание, что разница между крайними значениями будет другая, и для нас это важно.
Теперь разберем пример на python, смоделируем стократное подбрасывание монетки. Результат такой функции это сколько раз выпал орел. Эксперимент повторим 200 раз. Для каждого 200*100=20000 суммарно попыток. Результат в виде списка 50, 46, 53, 48…47, 53, 49.
import numpy as np # n - число испытаний # p - вероятность появления события np.random.binomial(n=100, p=0.5, size = 200) |
Еще пример: в урне 8 шаров, 5 белых и 3 черные. Наудачу вынимают 3 шара, надо найти закон распределения количества белых шаров в выборке. Вытянуть все черные шары можно только в одном случае. Всего случаев может быть 56, так как искомое значение из 8 по 3. 8* 7 *6 / 6 = 56. Значит вероятность, что x=0 составляет 1/56.
Что мы можем делать со случайными величинами: их можно суммировать, например просто Z = X + Y. Вытянуть один белый и два черных шара интерпретируется как 1 из 5 и 2 из 3, или 15/56. Вытянуть два белых и один черный шан же это 30/56, и вытянули только белые = 3 из 5 или 10/56. Все это легко складывается, 1+15+30+10 = 56/56.
Другой пример, более методологический. ABC-анализ, который работает по принципу принцип Парето — 20 % всех товаров дают 80 % оборота. В сегменте A заложены самые частотные товары. В сегмент B уходят товары, которые дают 15% дохода, и в C уходит остальной товар, огромная куча товаров с минимальным доходом. + добавляем коэффицент вариации на стабильность спроса.
Векторы. Основные понятия
Вектор в школьной гемотериии это направленная линия со стрелочками, В линейной алгебре: элемент векторного пространства с множеством свойств. В Python: числовой массив (например, массив NumPy). Технически Вектор — это вообще любой набор чисел, записанных в определённом порядке (в столбик или в строчку). Запилим одномерный массив numpy, и посмотрим размерность.
import numpy as np s=np.array([33,54,24,76,46,44]) r=np.array([32,-22,12,0,74,-3]) d = r*s d len(d) |
Такой вектор можно складывать, вычитать, умножать на скаляры. Для сложения надо задавать вектора именно как массивы, а не просто списки list. Пропорциональность в математике обозначается специальным знаком||. Перейдем к задачам, в первой надо найти линейную комбинацию трех заданных векторов с тремя заданными коэффицентами: умножаем каждый вектор на соответствующий ему коэффциент и складываем то, что получилось. По условиям задачи, коэффиценты 300, 200 и 2.
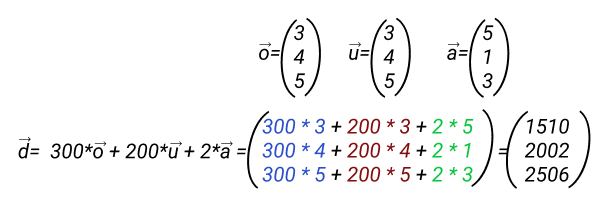
У нас есть промышленное предприятие, с тремя статусами критичности ассета: critical с весом в 1000, warning с весом 500 и info с весом 200. В течении месяца по каждому ассету было 10, 12, 15 critical, 21, 34, 12 warning и 100, 200, 300 info. Давайте считать:
critical = ([10,12,15]) warning = ([21,34,12]) info = ([100,200,300]) #нужно найти линейную комбинацию трёх векторов показов с коэффициентами critical = np.array([10,12,15]) warning = np.array([21,34,12]) info = np.array([100,200,300]) vd = 1000 * critical + 500 * warning + 200 * info vd |
Результат array([40500, 69000, 81000]).
Data-Oriented
Популярный ныне Data-driven заключает в себе одну простую идею: в любой момент времени знать ответ на три вопроса, где я сейчас, куда я стремлюсь и движемся ли мы в нужном направлении. Правильнее называть этот подход Data-Oriented. Для начала цель, куда мы движемся, это видение продукта гейм-дизайнером или продуктовым дизайнером. Состояние: смотрим на данные (логи игроков) и статистику. И знание, куда мы идем — обычно самое сложное. За третьим пунктом скрывается понимание, как цифры друг с другом коррелируют, где мы растем, где падаем, какие гипотезы побеждают и почему.
Для сбора данных нужно логирование и разведочный анализ: некий специалист раскладывает игру на механики, механика бьется на шаги для эвентов, для каждого шага выделяется список параметров поведения игроков. И прикидываем, что общего из профиля игрока нужно взять для понимания взаимодействия с механикой. Например, у нас есть ежедневные задания по открывают сундучков. В задании три события: открыть окно, увидеть квест, скликнул награду. У каждого события есть параметры: размер награды, время просмотра, кол-во золота у игрока, время суток и так далее. Это важно, многие аналитики не понимают, что технические логи не тоже самое, что и игровые эвенты. Нельзя полагаться только на технические логи сервера, они оторваны от логики игры.
Как частотный пример это события-тикеты. Игрок завершил уровень в игре, но те, но нам важны и те, кто не смог завершить уровень. Игрок провел 3 сек на уровне, и мы посылаем информацию на сервер, что происходило с ним, какие значения и клики повлияли на его провал на уровне.
Для больших эвентов надо подтягивать очень много параметров, например, уровень героя, платящий/неплатящий игрок, платформа, возраст игрока (разный возраст = разный гемплей), включайте все глобальные сегментации в каждый эвент.
Итак, мы готовим акцию к запуску, типичная распродажи лутбоксов. Для начала выбираем правильное время, кол-во игроков в онлайн в пятницу вечером самое большое и стабильное. Смотрим баланс валюты по уровням, спрос на товар рассчитывается по коэффиценту вариаций. И заранее думаем, как будем считать итоги акций: надо слегка подождать, не начинать считать результаты сразу после акции. Строим узкий доверительный интервал, и ждем сколько-то дней, чтобы доход вернулся в норму по сравнению с тем, что был до запуска акции. После делаем выводы, сколько товара люди купили, сколько мы потеряли после акции, так как люди начали покупать меньше (ведь уже закупились по акции), вычитаем одно из другого. Помимо этого, можно проанализировать поведение отдельно платящих и неплатящих после окончания акции, поведение игроков с максимальной наградой, траты софт-валюты.
Пример, как можно сделать рекламу в игре или продукте. Запускаем a/b-тест баннера, для каждого баннера считаем CTR (Click-through rate). Оцениваем доверительные интервалы, и если они пересекаются, то мы не имеем права делать выводов, нет статистической значимости. Если не пересекаются, то берем z-критерий, и проверяем, что доли не одинаковые. Далее считаем z-статистику, p-value. Не забываем про случайные клики, с фродом надо бороться. Либо эвристика, когда прописываем правила что клик должен быть после появления баннера на странице, до глубокого ML.
Еще один инструмент работы с восприятием это комбинаторика. Человек в казино видит, что несколько раз подряд выпало черное, значит, сейчас надо ставить на красное. Это называется здравым смыслом, и это ловушка нашего мозга, так как у каждого нового розыгрыша шансы по прежнему 50/50. Если в игре указано, что шанс нанести критический удар 25%, то это не значит, что каждый четвертый удар будет критом. Или у игрока 50% шанс получить редкого героя из лутбокса и две попытки открыть лутбокс. У четверти игроков в обоих случаях не выпадет редкого героя, игроки обидятся и уйдут из игры, хотя здравый смысл считает шансы 50%+50% = 100%. По этой причине в играх далеко не всегда используется честная вероятность, для избежания негатива.
Углубляясь в комбинаторику, есть несколько типов событий. Существует понятие случайного события, в классической комбинаторике случайное событие это то, на вероятность которого мы не влияем (какая карта выпадет). Независимые события—те события, которые случаются независимо друг от друга. Пример: достаем из колоды одну карту, затем еще одну карту, и это зависимые события, так как каждый раз уменьшается количество карт.
Несовместные события, это когда одно событие иключает появление второго события. Если мы уже вытащили тройку бубен, значит, второй такой карты уже не будет.
Формула Бернулли описывает вероятность срабатывания события А определенное количество раз при нескольких независимых испытаниях. Позволяет не производить огромного количества вычислений. Например, можно легко выяснить шанс получить определенный игровой предмет или скидку. У Бернулли события независимы, в Google Sheets легко реализовать с помощью COMBIN и POWER, решение довольно изящно и, как я люблю, быстрое в реализации.
Если события не независимые, то используем гипергеометрическое распределение. Например, игрок вытащил одну карту из колоды, в колоде остается 59 карт,то есть их стало меньше. Это прямая зависимость. Позволяет рассчитать, с какой вероятностью из колоды N можно можно вытащить карту M.
Матрицы
Работая с данными, вы неминуемо столкнетесь с матрицами. Матрица представляет собой набор чисел, расположенных по строкам и столбцам, как в таблице. Например, матрица на 3 строки и 5 столбцов, такая матрица называется 3 × 5 . Типичная запись положения одного элемента в матрице выглядит как а31 , где первый индекс 3 отвечает за номер строки, второй 1 за номер столбца.
Матрицы могут отличаться по содержанию:
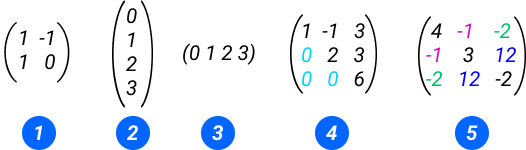
- Квадратная матрица второго порядка
- Вектор-столбец
- Вектор-строка
- Верхнетреугольная квадратная
- Симметричная-квадратная
Складывать и вычитать можно только матрицы одинакового размера, поэлементно. Умножение матрицы на скаляр аналогично векторной операции и работает поэлементно. Числовые множители также можно выносить из матрицы. Но это все укладывается в здравый смысл и ту часть математики, в которой нету букв. Интереснее посмотреть транспонирование матриц, Если транспонировать вектор-столбец, получится вектор-строка и наоборот:
import numpy as np A = np.matrix("1,2,4,7;-3,43,0,3") v = np.array([7,5,1]) print(A) print(v) print(A.T) print(v.T) |
Обратная матрица. Обратным к числу а называется такое число a -1, которое в произведении с a даст единицу. Обратные числа есть у всех чисел, кроме нуля. Например, для 2 обратным будет 0.5: 2 -1 = 0.5, т.к. 2 · 0.5 = 1.
Определитель матрицы А обозначается как det (A). например, определить, куда смотрит виртуальная камера. Мировые координаты записаны как три вектора, определитель бывает только у квадратных матриц. Чем ближе определитель к нулю, тем труднее высчитать обратную матрицу.
import numpy as np A = np.matrix('2,7,4; 4,4,7; 2,5,7') np.linalg.det(A) |
Определитесь произведения равен произведению определитиелей и не зависит от порядка умножения. Произведение определителя и обратных матриц равняется единице. Определитель диагональной матрицы равен произведению диагональных элементов.
Визуализация
Данные важно уметь визуализировать. Визуализация: excel (умеет делать запросы во внешние базы данных), Power BI, Tableau, Python/R, Google Data Studio и многое другое. Конечно, следует сказать, что инструмент не важен, мне удавалось делать крутые дашборды на Grafana. Главное результат, но тем не менее, в перечисленных инструментах получить результат сильно проще. Разберем некоторые базовые графики.
Первый в списке это Line Chart, простой линейный график. Лучше всего описывает течение некого процесса во времени. Визуально, линии лучше делать достаточно толстые, не более 4-х линий на одном графике. Не забываем указать легенду для цветов, подписывайте оси и размерности. Если данные шумные, то берем простое скользящее среднее, и получаем тренд. Цвет может подсказывать пользователю о степени важности значения, так, обычно желтый цвет означает низкую степень серьезности, оранжевый — среднюю, а красный — высокую. Зеленый цвет часто используется для индикации низкой нагрузки или отсутствия угроз.
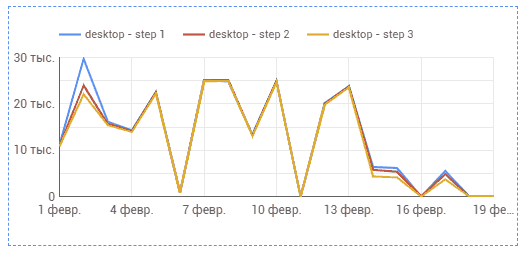
Вторым номером идет столбчатый Bar Chart. Классическое складывание друг на друга нескольких величин позволяет увидеть распределение. График с накоплением подразумевает, что в самый низ ставят самое важное значение. Не нужно путать Bar Chart и гистограммой (не смотря на мнение русской версии Excel). Гистограмма используется, когда нужно показать частотность распределения величины по интервалам и может быть только вертикальной. Бар-чарт может быть и горизонтальным. У гистограммы сведен к минимум интервал между значениями. Обычно поверх столбцов накладываются полосы погрешностей для обозначения стандартного отклонения, стандартной ошибки или доверительных интервалов.

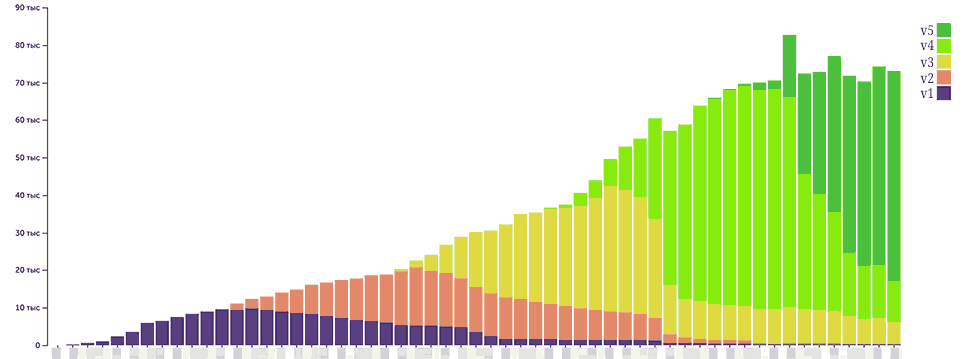
Если объединить Line chart и Bar Chart вместе, то мы увидим воронку. На воронках хорошо виден кумулятивный рост оттока, можно наглядно увидеть, сколько потеряно людей (Churn Rate).

Если каждый столбец будет отвечать за определенную дату во времени, то это уже Time-series plots. По одной оси отоброжается время, а значение каждого элемента данных указывается по другой. Например, мы можем использовать график временного ряда для отображения роста численности населения города с течением времени.
Гистограмма. Простой и понятный график, отвечает на вопросы типа «за сколько ходов игрок заканчивает уровень», «сколько сундуков открывает до выпадения героя-танка». Технически, это множество столбцов, которые отображают частоту появления значений в наборе данных. Каждый столбец представляет значения в определенном интервале. Они представляют собой полезную визуализацию для проверки распределения данных и позволяют легко обнаружить провалы. Определение оптимального размера интервала (bin) может оказаться непростой задачей, поскольку оптимальные размеры бина зависят от конкретных данных. Гистограммы обычно используются для визуализации формы, симметрии и перекоса базового распределения данных. Понимание распределения данных необходимо для дальнейшего анализа и определяет типы статистических методов, которые мы можем применить к данным.
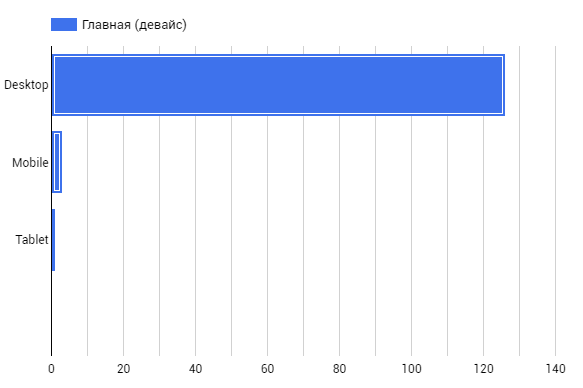
100%-ая столбчатая комбинированная диаграмма. Используется для описания структурного процесса конкретного показателя. Вам нужно показать развитие процесса и показать общий тренд процесса. Изменение величины по истечению времени, как LTV меняется с lifetime.
Диаграмма рассеивания нужна для поиска корреляции между двумя переменными, например, насколько кол-во побед влияет на retention игрока. Визуально это математическая диаграмма, изображающая значения двух переменных в виде точек наплоскости. Можно добавлять дополнительные переменные, используя цвета (scatter chart) или размер (bubble chart). Используется для поиска взаимосвязи или корреляции двух переменных. Чаще всего это выражается как результат пользователя (процент побед + нанесенный урон + полученное золото) в зависимости от двух разных игровых параметров, выражаемых численных количеством. Более технически, диаграмма рассеивания показываем значения двух переменных, отложенные по двум осям. Такой график сложен для интерпретации начинающими пользователями, так как они требуют длительного обучения, но могут быть очень эффективны для опытных пользователей, так как закономерности позволяют сразу понять суть проблемы.
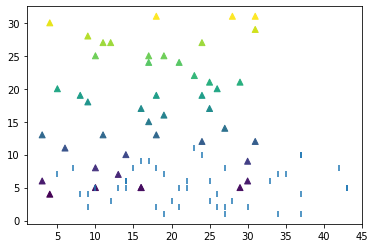
Также, бывает сложен для восприятия parallel coordinate plot, который отображает метрики в наборе данных. Предположим, что у вас есть БД с метриками. Каждое значение каждой метрики является точкой на соответствующей метрической оси. Такой график позволяет показать взаимосвязи в многомерных наборах данных. Однако помним о трех ключевых моментах:
- порядок расположения каждой оси влияет на интерпретацию визуализации
- каждая метрика должна быть нормализована
- большие наборы данных приводят к появлению большого количества шума в визуализации.
Радарные диаграммы (Radar chart / Spider chart), показывает многомерные данные с помощью нескольких осей в круге, причем длина осей пропорциональна значениям данных. Расстояния между секторами каждой оси равномерны.
Теория игр
Это прикладная математика про стратегическую игру в социуме. В жизни игроки далеко не всегда принимают рациональные решения, и теория игр как раз про взаимодействие в таких условиях. Если вы помните фильм «Игры разума», то там есть персонаж Джон Нэш, известный благодаря равновесию Нэша. В целом, теория игр учит нас устанавливать правила игры и стратегически манипулировать. В теории игр обязательным условием является социальное взаимодействие, так как успех игрока напрямую зависит от остальных игроков. Выбор товара в магазине в одиночку — не игра, нет второго участника. А вот выбор товара с женой или ядерное противостояние сверхдержав — уже игра.
Самая типичная задача это «дилемма заключенного». Два преступника совершили ограбление и были пойманы. Следствию нужно доказать, что они работали в сговоре. Полиция разводит людей в разные камеры и каждому предлагает одну и ту же сделку со следствием: сдать напарника и уменьшить срок пребывания в тюрьме. Если первый заключенный предает второго, то второй идет в тюрьму на 10 лет, а первый освобождается за помощь следствию. Молчат оба — оба получают срок по легкой статье, если оба придают друг друга, то оба получают по 5 лет тюрьмы. В итоге, у каждого заключенного есть два варианта, промолчать или сдать напарника.

Итак, для начала введем понятие доминирующей стратегии. Это та стратегия, которая лучше для игрока, все зависимости от действий других игроков. Рациональный игрок выберем именно её. И второй вид стратегии, доминируемая стратегия — та стратегия, которая отличается от доминирующей, её игрок будет стараться избегать. Первый игрок имеет доминирующую стратегию предать второго игрока, второй игрок аналогично, будет иметь доминирующую стратегию предать первого игрока.
Дилемма в том, что если оба предадут друг друга, то оба проиграют. А если оба промолчат, то оба условно выйграют. И ни один игрок не может изменить свою стратегию, не ухудшив ситуацию другого игрока. Некий парето-оптимальный подход. Предать/предать не является парето-оптимальный, так как он не оптимален в данной ситуации. Это история про то, что кооперация дает плюсы, но взаимное недоверие все портит. И именно поэтому теория игр не является хорошо предсказывающей поведение, реальное поведение сильно отличается от предсказанного теорией.
Второй пример теории игр это игра в мафию. Игроки: горожанин, мафиози и маньяк. Горожанин честный, маньяк всех убивает, мафиози просто преступник. Побеждает тот, кто к утру остался жив. Наступает ночь, просыпается мафия и соревнование идет между мафиози и маньяком. У обоих одинаковый выбор, убить мафию/маньяка или мирного жителя. Если маньяк и мафия убьют друг друга, то выйграет мирный житель, если мафия убивает маньяка, а маньяк убивает мирного жителя, мафия выигрывает. Если маньяк убивает мафию, а мафия мирного жителя, маньяк выигрывает. Если же просто убить мирного жителя, то у мафии и маньяка ничья.
Итак, тут стратегия мафии не зависит от стратегии маньяка, мафия будет хотеть убить маньяка, тогда она победит. Можно договориться и убить мирного жителя, тогда будет ничья, но так как соглашение между сторонами отсутствует, то хороший исход для обоих сторон невозможен, как часто и бывает в реальной жизни.
Разберем схожий пример из жизни. Он не совсем про теорию игр, но тоже про восприятие и интерпретацию внешних данных. Вы выйграли в лотерею, и вам пообещали дать $500,000 через 3 года, но компания предлагает выкупить это обещание. Они вам заплатят здесь и сейчас, вы боитесь что компания не выполнит обязательства через 5 лет и не даст вам денег. Но сколько они должны заплатить? Текущая ценность = $500,000/(1+0.1)⁵ = $500,000/1.61 = $310,559.
Кажется, что потеряться почти $200,000 это ужасно, но деньги нужны сейчас. Но деньги можно положить в банк под процент. У нас есть k = 500.000, процентная ставка 0.1% на 5 лет. Это означает, что сегодняшние наши $310 599 под 10% годовых и в течении 5 лет как раз превратятся в $500 000.
Сказки
Геймификация и игрофикация это не только про цифры. Цифры должны быть интерпретированы на культурные особенности и паттерны людей. Для начала, поговорим про философа и историка Йо́хана Хёйзинга, современник Карла Густава Юнга, который написал трактат «Человек играющий». В трактате собраны все ключевые базовые мифологии из культуры множества наций, в которых была выявлена общая структура с точки зрения игры. При этом мы не рассматриваем игру как программный продукт, играми также являются спорт, политика, деловые отношения. Приметы игры по Хёйзингу:
- у любой игры есть участники;
- есть начало и конец;
- любая игра вне объективной реальности и не пересекается с обычной жизнью;
- в игре есть свобода действий;
- игра определена местом, локацией;
- игра детерменирована временем;
- у игры есть правила, которых придерживаются все игроки, или вылетают из игры.
Вторая знаковая личность в структурировании паттернов поведения из сказок это Владимир Яковлевич Пропп и его «Морфология «волшебной» сказки». Это сильная исследовательная работа, которая доказывает, что сказки можно преобразовать в математическую формулу. Он выяснил, что в нескольких сотнях сказок очень схожий базовый сценарй, и у разных народов мифиологические элементы едины. Все сказки это производная от мифологии. Архетипы и сюжетные линии сказок укладываются в следующую структуру:
- главный герой вынужден покинуть родной край;
- некто предлагает герою испытания;
- герой получает приз за испытания;
- сражается с главным боссом;
- получает главный приз;
- возвращается домой;
И третий важный автор это Джозеф Кэмпбелл, и его книга «Тысячеликий герой». Суть книги простая и схожая с перечисленными выше. У всех мифов прослеживается единая структура и цикличность, которые он назвал «Мономиф». И именно на основе работ Джозефа Кэмпбелла, легендарный Джордж Лукас довел до ума сюжет первой трилогии Звездных Войн. Мономиф состоит из трех больших шагов: сепаративная стадия ->лиминальная стадия ->восстановительная стадия.
Герой начинает путь с сепаративной стадии, в которой присутствует расставание с домом, с зоной комфорта и переход в новый, жестокий и напряженный мир. Герой обретает защитника, наставника, помощника, в общем, новых друзей. Далее идет лиминальная стадия, вв течении которой герою нужно пройти точку невозвата, окончательно отделяющую его от привычной ему жизни. Он проходит множество испытаний, монстров, сложных вопросов и решений, и побеждает финального босса. Босс не обязательно монстр, боссом может быть любое олицетворение изменения характера героя (был слабый — стал сильный, был трус — стал смелый, был неудачник — стал победитель). И восстановительная стадия, в которой герой возвращается к оригинальной точке зоны комфорта, и передает свои новые навыки и достижения друзьям. В итоге, наблюдатель испытывает настоящий катарсис.
Метод Монте-Карло
Если вспомнить пример, когда несколько раз подряд выпало черное, то в противовес заблуждению можно поставить метод Монте-Карло. Это метод приближенных вычислений, весьма полезен, когда условия задачи очень быстро и часто меняются. π ≈ 3,14, это приближенное значение. Метод Монте-Карло это не четко определенная группа методов для изучения случайных процессов. Монте-Карло используется для описания любого подхода к оценке, бизирующейся на случайной выборке. Модель симулирует множеством случайных сигналов с заданной плотностью вероятности. Целью является статистическое определение результатов на выходе.
Самый частотный пример это нахождение геометрической вероятности в задаче Бюффона про бросания иглы и нахождения числа π, основан на методе Монте-Карло. Берется игла и бросается на поверхность, на которой нарисованы две парралельные прямые линии, расположенными на расстоянии друг от друга. Задача сводится к нахождению площади.

Как использовать на практике: есть два игрока, которые друг друга атакуют по очереди. Проводим много боев и выводим средний результат. Количество нужных испытаний зависит от функции распределения (коэффициент Лапласа в помощь). Сначала должно быть две глобальные переменные, и понадобится много испытаний для достижения достаточной точности.

14 комментариев
Vadim Filimonov
Как LTV считается?
Цветков Максим
LTV сочетает в себе многие метрики. Планировать LTV = прогнозировать доход, что не самая простая задача. Итак, есть много способо подсчета LTV, например, берем Total Revenue за весь период, Total Unique Users за весь период и делим друг на друга. Это самый простой способ и очень не точный, есть посложнее.
Lifetime (среднее время от установки до неактивности) + ARPDAU (или ARPU). Понадобится выбрать период неактивности, например, 14d пользователь не возвращался в проект, считаем что он ушел. И третий вариант это ARPDAU * Lifetime (Lifetime это интервал по retention).
Это один из простых способов: lifetime * AD ARPDAU. Lifetime может быть интеграл от retention или все время от установки до неактивности. AD ARPDAU вам скажут рекламные сети. Да, ARPDAU может быть не постоянным, lifetime это информация из прошлого.
Другой простой способ подсчета LTV = lifetime * ARPU. Сложный LTV = интеграл от функции retention * ARPU.
Один из примеров расчета:
YouTube:
Paying Users 1mo: 10 000
Revenue 1mo: $325 584
ARPPU: $59.8
Lifetime: 4
Итого User LTV: $59.8 * 4 = $239.2
Как косвенная метрика, можно грубо прикинуть продолжительность жизни пользователя. Например, Monthly Active Users = 200 000. Коэффициент оттока пользователей колеблется вокруг 4,3%. Средняя продолжительность жизни пользователя при известном коэффиценте оттока считается по геометрической прогрессии, если они уходят равномерно. Или по очень примерной формуле 1 / 4,3% = 23 месяца, то есть почти два года. Обычно отток для пользователей не на контракте это LTV = средний доход с клиента / churn rate. Так как в этом случае отток трудно определить: на контракте отток это расторжение договора, а без контракта это перестать посещать магазин/приложение. Правильный подход это beta-geometric или небинарное распределение. Все пользователи делятся на живую и спящую стадии, у живых кол-во покупок должно соответствовать распределению Пуассона с лямбда коэффицентом скорости транзакции.
Это для живых проектов, если же проект еще не запущен, то метод аналогов: найти похожие проекты и смотреть бенчмарки.
Yury Grigoryev
Добрый день, как сравнивать два разных визуала, каким методом? понимаю, что a/b, но ведь можно и по какой либо другой методологии пойти же?
Цветков Максим
A/B в данном случае сложновато, как мне кажется. Ведь почти наверняка трафик небольшой, времени мало, метрика — конверсия. При таких вводных приходится бустрепить, постстратифицировать, работать с многорукими бандитами или уменьшать дисперсию теста с помощью CUPED. + ускорять тесты линеаризацией, за счет меньшего кол-ва семплов. Если пойдете по этому пути, то sequential testing через частотный подход, байес позволяет ввести стоимость потери в случае ошибки и не превышать заданную границу.
Можно простым опросом, показать две картинки и попросить выбрать ту, которая понравилась + добавить оценку по шкале от -3 до 3 и открытый вопрос. Либо аналогично, но показывая лишь по одному варианту каждому респонденту, тогда «контраст» между результатами будет меньше.
Я иногда выкидываю ответы тех, кто не написал ответы в свободной форме или написал нечто вроде «ttttt». Комменты надо вычитывать и отделять факты от флуктуации. Например, 5% комментов из 6000 про негатив о сервисе, значит это факт, 5 комментов из 6000 про негатив — флуктуация.
Eugene Karambirov
Привет! а есть способ померить степень потерянности человека в продукте? Не привносят ли такие улучшалки дополнительного блуждания по структуре сервиса?
Цветков Максим
Можно посмотреть в сторону KLM, GOMS или SEQ. В первом приближении, задача про замерить количество кликов, времени, и пройденных страниц для идеального варианта выполнения сценария, заложенного проектировщиком, и для реального. И сравнить, посматривая на метрику error rate. Получится нечто вроде lostness.
Формула lostness:
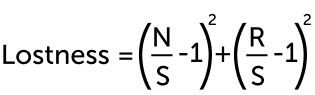
N — количество посещенных уникальных страниц за сессию выполнения задания
S — количество посещений не уникальных страниц за сессию выполнения задания
R — сколько страниц заложено для выполнения сценария проектировщиком
Mikhail Uhabov
Часто в результатах исследований пишут, что не была достигнута статистическая значимость. А всегда ли вообще есть возможность получить статистически значимые результаты? Может, выборка изначально была меньше нужной.
Цветков Максим
Для ответа на вопрос надо искать статистическую мощность. Статистическая мощность это вероятность не пропустить эффект, когда он правда имеет место быть. На языке формул это (prob = 1 — β), когда мы отвергаем нулевую гипотезу, и она правда не верна. Для подсчета статистической мощности нужно знать размер выборки, уровень статистической значимости, и минимальный размер эффекта, который мы ожидаем.
Про размер эффекта надо поговорить отдельно. Это не техническая история, а больше из мира психологии. Мы должны не просто понимать, будет ли эффект или нет, но и насколько значимым должен быть эффект. Если мощность низкая, то мы не заметим даже большой эффект.
Существует правило большого пальца Коэна для размера эффекта:
Два самых простых способов измерения эффекта ялвяются Пуассон и Коэн. Посмотрим поближе на Коэна:
И далее считаем из t-test’а. Вторая формула это на случай, если речь о стандартных ошибках, а не об стандартном отклонении.
Все знают что уровень значимости обычно 0,05, то есть 1 ошибка из 20 случаев. Для ошибки второго рода риск должен быть весьма высоким. Ошибка первого рода в четыре раза опаснее, чем ошибка второго рода. Допустимый риск ошибки второго рода это 1 к 5, или 0,2. Отсюда и общепринятая статистическая мощность 1 — 0,2 = 0,8. Чем опаснее может быть ошибка (ядерная энергетика, космические корабли), тем меньшие значения вероятности допустимы. Чем больше выборка, тем выше мощность.
Альфа — вероятность, с которой мы согласны на допущение ошибки первого рода (тот самый уровень значимости 0,05). Если α (вероятность ошибки первого рода) увеличивается, то β (вероятность ошибки второго рода) уменьшается. Мощность: 1 — β, при увеличении значения α уровень значимости слабеет, и растет статистическая мощность для нахождения эффекта в эксперименте. Чем более высокий уровень значимости мы зададим, тем меньше шансов получить значимый результат и уменьшится статистическая мощность.
Для сравнения различных выборок применяются двусторонние тесты. Если используем односторонний тест, то удваиваем коэффицент ошибки (ошибка первого рода) параметр α, для одностороннего теста α = 0.20, α = 0.10 для двустороннего.
Mikhail Uhabov
Здорово, спасибо!
Как тогда определить размер выборки для парного теста?
Цветков Максим
Формулы по определению размера выборки отличаются. У нас выборки парные, не независимые. Парные выборки это состоящие из одинаковых объектов исследования, обследованных в разные моменты времени. Пациенты до и после лечения, поведение постоянной аудитории до и после редизайна. Для нахождения достоверного различия между двумя парными выборками нужна такая формула:
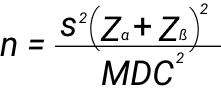
n - размер выборкиs - стандартное отклонение
Zα - коэффициент ошибки первого рода (см. таблицу ниже)
Zß - коэффициент ошибки второго типа (см. таблицу ниже)
MDC (Minimum detectable change size) - минимальный эффект, который мы ожидаем обнаружить.
Указывается абсолютными значениями. Мы хотим обнаружить изменение в 40% в среднем значении выборки в текущем году относительно предыдущего, и среднее значение за предыдущий год — 200, считается так: MDC 0,4 * 200 = 80.
Таблица стандартного нормального отклонения для Zα:
Стандартная ошибка считается как z-score 1.64 (для 90-процентной доверительной вероятности) и увеличивает значение ошибки. Чем больше число, тем больше доверительная вероятность, то есть наша уверенность в корректности результата. Стандартная ошибка зависит от уровня доверительной вероятности, дисперсии и от размера выборки. Большая дисперсия = бОльшая ошибка, и чем больше выборка, тем меньше шанс ошибки. Поэтому мы стремимся к большой выборке и маленькой дисперсии. Выборка должна быть от 1 000.
Если надо отслеживать изменения с течением времени в одинаковой выборке в рамках одного года, тогда не будет стандартного отклонения между парными образцами.
Mikhail Uhabov
Я забыл сказать, что получаю уже агрегированные данные и работаю со средним значением в выборке. Как мне в таком случае узнать необходимый размер выборки?
Цветков Максим
Так. Задача на определение необходимого размера выборки для оценки среднего с заданным уровнем значимости. Предположим, что мы работаем со средним значением в выборке. Начальный размер выборки высчитывается по следующей формуле:
n - предварительная оценка размера выборкиZα - стандартный коэффицент ошибки (см. таблицу ниже)
s - стандартное отклонение
Про B поговорим подробнее. Это желаемый уровень точности, выраженный половиной максимально допустимой ширины доверительного интервала. Указывается в абсолютном выражении. Мы хотим получить ширину доверительного интервала в пределах 20% от среднего значения выборки, и среднее значение 60 яблок на ветке, значит B = 0.2*60 = 12.0
Таблица стандартного нормального отклонения Zα:
Следующий шаг это коррекция размера выборки. И еще один шаг — дополнительная коррекция, так как формула выше предполагает, что вся популяция намного больше той, которую мы берем в качестве примера. Если выборка составляет более 5% совокупности, то к оценке размера применяется поправка (FPC).
Mikhail Molovtsev
Привет! при запуске a/b теста аудитории пересекаются. Как это компенсируется? знаю что не должны пересекаться, но инфраструктура и бизнес этого не позволяют
Цветков Максим
Вопрос очень широкий. Первое это CUPED как предиктивный алгоритм. Например из недавних задач: рекламная кампания на автобусных остановках в Дубае. Хотелось узнать, насколько эффект повлиял на выручку в конкретных районах с остановками. Очевидно, что все пользователи смогут увидеть рекламу во время перемещения, нет контрольной выборки. И объектами являются территории, а не люди. Предиктивный CUPED позволяет прогнозировать целевую метрику за экспериментальный период, то есть можно посчитать ожидание по метрике и сравнить с реально полученным значением. И в итоге мы сравниваем территорию с тестом и без него.
Либо interaction effect. Когда один отдел компании заводит тест на купоны в корзине, а второй отдел делает разные рассылки разным пользователям. Каждая гипотеза от отдела сама по себе могла бы выйграть, но суммарный эффект дал негатив. Тут все просто — не запускать два теста одновременно. Потому что в тестах на взаимодействие невозможно интерпретировать влияния факторов самих по себе.