Python в анализе тестов
Принимать решения без данных это как играть в русскую рулетку: повезет – не повезет. Поэтому данные нужно копить с первого дня жизни бизнеса. Данные это сырье для бизнеса, и по началу они будут помогать принимать решения без особых затрат. Но когда количество данных перевалит за 1 Tb, бизнесу станет сложнее быстро выжимать фичи по векторам на регулярной основе. Помочь может визуализация данных. Имея в багаже математическую базу и возможности Python при использовании библиотек matplotlib, seaborn и plotly, можно покрыть большинство потребностей по визуализации графиков для руководства и для принятия решений.
Существует множество инструментов для визуализации данных: R, Python, JS, Matlab, Scala и Java. R это больше язык для исследователей и студентов, поэтому у него на данный момент больше полезных библиотек для визуализации, чем у Python. Но Python лучше для дальнейшей интеграции разработки.
На больших проектах, где положительные изменения дают 1%<, аналитика необходима. Как минимум, нужно не только проверить результаты a/b теста, но и как эти две группы пользователей вели себя до эксперимента. И отсечь влияние других экспериментов, прошлых и нынешних.
Примерный пайплайн такой:
— проверяем данные на нормальность;
— проверяем отличия с помощью статистического теста;
— доверительным интервалом оцениваем масштаб (среднее при нормальности или медиана для ненормальности данных);
— сравниваем с прошлым поведением групп пользователей;
Данных для визуализации на Python должно быть много, иначе нет смысла в распределенном анализе. Если данных много, то вы почти всегда получите маленькое p-value, и вам останется только проработать нормальность данных, их независимость и т.п. Для расчёт размера выборки нужны тесты для анализа мощности (power tests). На маленьких выборках статистические тесты могут быть менее эффективны, чем экспертная оценка, а на больших данных будут видны даже минимальные отклонение от нормальности. Также, при малой выборке мы не можем использовать центральную предельную теорему.
Основная библиотека для визуализации это Matplotlib. Отмечу, что Matplotlib пусть и очень популярная, но достаточно старая и сложная библиотека, и для комфортной работы лучше использовать API поверх Matplotlib, такие как Seaborn, у которого много своих способов построения графиков. При том, достаточно эстетичных. Достаточно добавить sns.set(), посмотрим на примере:
import matplotlib matplotlib.use('TkAgg') import numpy as np from matplotlib import pyplot as plt import seaborn as sns; sns.set() norm_data = np.random.normal(size = 1000, loc = 0, scale = 1) plt.hist(norm_data) plt.show() |
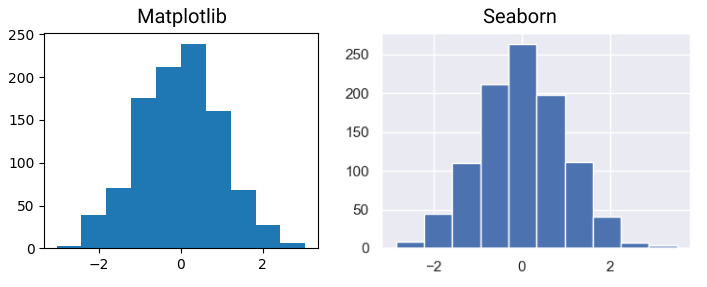
Мы построили наш первый график, используя Python. Конечно, хочется быстрее перейти от работы со списками к работе с массивами значений. Но для начала немного освежим теорию математической статистики:
Нулевая гипотеза всегда консервативна (проще проверяется), а альтернативная гипотеза это ненормальное распределение. В первую очередь проверяется нормальность данных, так как для среднего и стандартного отклонения нормальное распределение может быть лишь одно, ненормальных распределений возможно бесконечное количество. Проверка нормальности возможна тестом Shapiro-Wilk, который проверяет нулевую гипотезу о происхождении данных из нормального распределения. Есть понятие смеси распределений, в этом случае приходится обращаться к Марковской цепи Монте-Карло (MCMC).
Проверка результатов a/b-теста это частный случай проверки статистической гипотезы. Статистическая гипотеза это предположене о виде распределения и свойствах случайной величины, которое можно подтвердить или опровергнуть. По умолчанию требуется проверить гипотезу H0, это называется нулевая гипотеза. Она истинна, пока не доказано обратное. Если доказано обратное, то побеждает альтернативная H1 гипотеза .
Принято использовать следующие обозначения:
| Показатель | Генеральная совокупность | Выборка |
| Дисперсия | σ² | s² |
| Размер выборки | N | n |
| Коэффицент корреляции | p | r |
Генеральная совокупность и выборка. В чем разница? Выборка это набор данных, который у нас есть. Генеральная совокупность это вообще все данные, которые можно учесть при расчетах. Простой пример: у нас есть пирог, мы отрезаем кусочек и пробуем. Если торт вкусный, то на основании выборки (кусочка) мы делаем вывод про всю генеральную совокупность (торт).
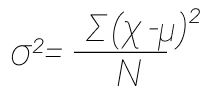
Например, у нас есть выборка из нормального распределения с неизвестным параметром α и известным параметром σ = 1. H0 = параметр α равен некому значению, при этом гипотеза создается еще до данных, а не является их следствием. Проверяя H0, мы по выборке считаем некое значение и сравниваем его с теоретическим. Когда мы рассматриваем выборку, допускаем отклонения от теоретических значений, так как среднее арифметическое никогда не бывает равно мат. ожиданию, оно будет отклоняться. И мы стараемся установить, какое отклонение полученного значения от теоретического мы готовы считать допустимым (незначимым), и какое отклонение нельзя списать на случайные факторы (значимое). Если отклонение значимо, тогда H0 отвергается. Отклонение не значимо, H0 подтверждается.
Коэффицент корреляции. Корреляция это взаимосвязь двух и более случайных величин. Корреляция бывает очень разной: сильной в разной степени, негативной. В интернете очень любят сравнивать две никак не связанные величины, например, количество zoom-митингов в Чите и проданных ножей в Алабаме. Причинно-следственной связи никакой, но может быть схожесть поведения показателей.
Для работы нам нужно:
- Определиться с H0 и H1.
- Мы предполагаем, что нулевая гипотеза верна, и задаем некую статистику (функция от выборки), обозначим ее как T. У нас есть нормально распределенная случайная величина с неизвестной дисперсией, тогда используется такая статистика:
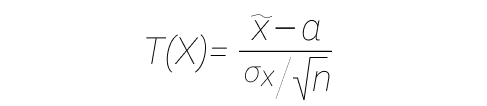
- В формуле выше статистика имеет распределение Стьюдента (t-распределение) с параметром df = n-1, где n — объем выборки. Если в формуле выше X имеет нормальное распределение, то такая статистика имеет распределение Стьюдента, мы берем это как доказанный факт. При нормальном распределении σ = 1, a = 0.
- Если известно мат. ожидание, а дисперсия не известна, и мы хотим проверить гипотезу о дисперсии, то берем квантили распределения хи-квадрат. Распределение хи-квадрат это другое распределение. Для большинства других распределений таких статистик нет. Например, выборочное среднее равномерного распределения довольно сложно считать, и мы считаем по ЦПД (число объектов в выборке = бесконечность, значит распределение близко к нормальному). Этим пользуются крупные компании, у них куча трафика. Если трафика мало, то можно заняться оптимизацией. Скорость a/b-тестов можно увеличить за счет управления чувствительностью тестов: оптимизация дисперсии, менять описательные статистики, трансформировать данные и изменять размерность данных (поубирали хвосты — дисперсия уменьшилась).
- Далее уровень значимости α — допустимая вероятность ошибки первого рода (те самые 0.05), значение варьируется в зависимости от задачи.
- Определяется критическая область. Ω = визуально это некий отрезок, который говорит нам о том, что значение T из пунктов выше попадает в критическую область.
- проводим статистический тест: для выборки считаем значение T (статистика, функция от выборки), и если оно принадлежит Ω, то считаем, что данные противоречат гипотезе H0 и мы принимаем H1.
Стандартное отклонение это квадратный корень дисперсии. Другими словами, это среднее значение квадрата разности значений в наборе данных от среднего значения. Если данные нормально распределены, то нужны среднее и дисперсия. Для проверки гипотез о дисперсии нормального распределения используются квантили распределения хи-квадрат. Остальные распределения, по большей части, не имеют соответствующих статистик, поэтому принято использовать центральную предельную теорему с некой погрешностью. На графиках выше и ниже вы можете видеть примеры визуализации нормального распределения.
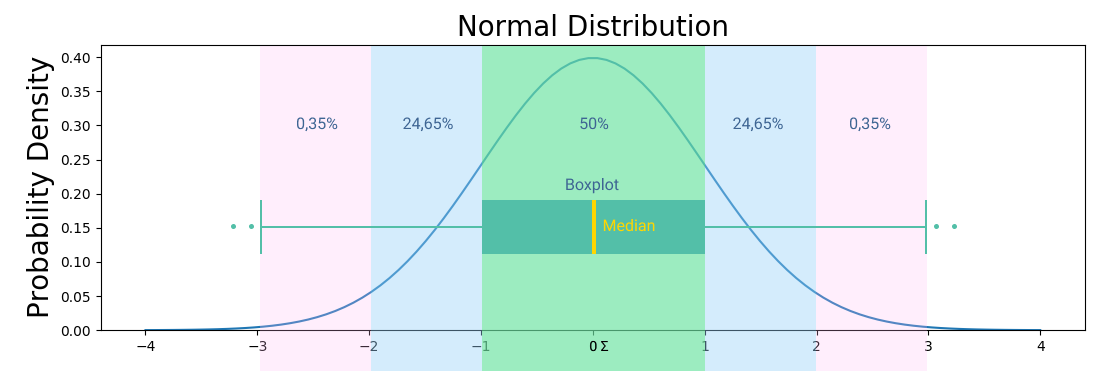
Среднее, медиана и мода это показатели центра распределения. А вариация распределения, изменчивость/волатильность выборки описывается параметром «Дисперсия». И тут в дело вступаем стандартное отклонение, это дочерний показатель от дисперсии. Показывает, на сколько в среднем отклоняются элементы выборки от среднего значения. Если средний китаец знает 3000 иероглифов, то стандартное отклонение 400 иероглифов. Если у нас среднее значение 100 заявок, а стандратное отклонение 300 заявок, то данные очень сильно колеблятся, это называется коэффциент вариации. просто делим стандартное отклонение на среднее и получаем на выходе %, так что это процентная величина отклонения.
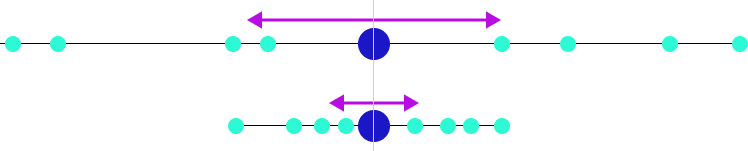
Дисперсия это не константа, с ней можно работать. Существует децильный метод. Мы берем все данные из теста и контроля и делим распределение на некое количество квартилей, децилей, перцентилей. Внутри каждого микро-набора данных будет своя размерность данных, по которому мы и будем оценивать эксперимент. 1-ая дециль будет содержать минимальные значения, 10-ая — самые большие. В таком подходе дисперсия уменьшается за счет уменьшения разброса данных. Необходимо использовать поправки на множественное сравнение: классический/консервативный Бонферони, метод Холма, Бенджамини-Иекутиели, Бенджамини-Хохберг. Или просто уменьшать p-value.
Если не хотим разбираться с нормальным распределением, то используем статистический метод бутстрэппинг.
На картинке вы можете видеть центральную линию, это медиана. Медиана это расстановка элементов выборки от меньшего к большему и берем самый центральный элемент выборки. Помимо удаления выбросов из данных, подсчета размера выборки, кластеризации группы пользователей, обычно всех интересует адекватная мера центральной тенденции, которая может быть представлена следующими понятиями:
- Среднее арифметическое значение в данных. Идея в том, что если взять любое типичное значение из набора данных, оно будет похоже на среднее значение. Не самый надежный способ, очень аффектится экстремально высокими или низкими значениями. 2+4+6+26 / 4 = 9,5, любимый подход недобросовестных СМИ.
- Медиана. В отличии от среднего арифметического, все значения сортируются в порядке возрастания и в качестве среднего значения берется то, что окажется в середине списка. Считается более надежным подходом, так как более робаста. Робастность = устойчивость к большим и малым значениям. Если в списке четное количество значений, то высчитывается среднее между двумя значениями из центра отсортированного набора данных.
- Мода. Значение, которое можно встретить в данных чаще остальных. Это менее среднее значение, чем два предыдущих. Скорее, это наиболее тяжеловесный фактор, который влияет на среднее значение в данных.
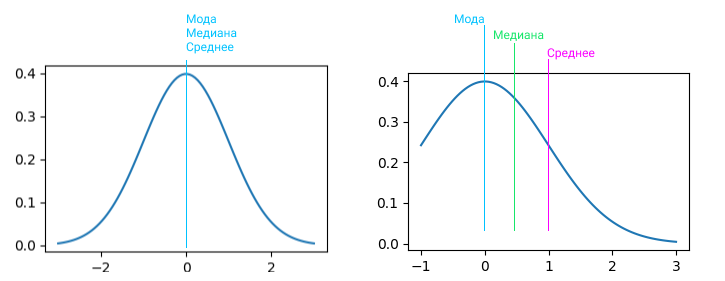
Разберем пример. Выбираем статистику, у нас гипотеза про математическое ожидание нормально распределенной случайной величины с известной дисперсией, вы берем чуть другую статистику (формулу), не такую как была в примере выше. Если H0 верна, то статистика (T) имеет нормальное стандартное распределение.
Нулевая гипотеза, что a = 6. Далее мы в рамках эксперимента нашли выборку, и хотим проверить гипотезу.
import numpy as np from scipy import stats data = np.random.normal(10,1,size = 200) data |
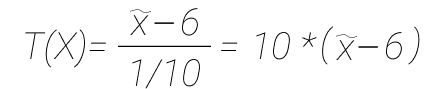
Далее работаем с критической областью. То, какую критическую область мы выберем, зависит от альтернативной гипотезы. Может быть двусторонней, левосторонней или правосторонней, в зависимости от задачи. В нашем случае значение может сместиться и на лево, и на право, поэтому выбираем двустороннюю критическую область. Выбрав двусторонний тест, мы задали условие для проверки гипотезы. Двусторонний тест не предполагает, что мы заранее знаем, какое значение будет больше, а какое меньше. Такой тест более консервативен и более общий, чем односторонний. Мы просто воспользуемся правилом двух сигм и получим интервал, или пользуемся таблицой квантилей. Квантили и квартили, тут все просто. Расставляем значения по порядку, например 100 элементов: 1,2,3….99, 100, и берем пятый квантиль — 5. Квартиль это частный случай квантиль, самые частотные квартили это 25%, 50% и 75%.
Найти квантили довольно просто: правило двух сигм дает интервал, в который с вероятностью 95% мы попадаем, и 5% что не попадаем. Квантиль будет 2 и -2. То есть, α/2 и 1-α/2, это квантили стандартного распределения. 2 и есть квантиль порядка 1-α/2, = 0.975. Теперь мы можем взять выборку, вычислить от нее значение статистики (T), и при попадании в критическую область отвергаем H0. Освежим в памяти сигмы: три сигмы это 99,73%, две сигмы это 95,45%, одна сигма это 68,27%.
Считаем мат. ожидание, mean = data.mean(). Результат 9.9296. И статистика: T = 10 * (mean - 6), результат 39.2962. Наша критическая область от бесконечности до 2 или от -2 до минус бесконечности, значение попало в область. Мы отвергаем гипотезу. Тут дело в том, что чем меньше α, тем шире критическая область, так мы можем управлять точностью теста и шансом отвергнуть гипотезу. И давайте пример посложнее:
import matplotlib matplotlib.use('TkAgg') import scipy.stats as stats from matplotlib import pyplot x = stats.norm.rvs(loc=5, scale=3, size=543) print (stats.shapiro(x)) pyplot.hist(x) pyplot.show() |
Я осознанно не использую seed, так как чем больше вариативность полученных вами результатов, тем лучше. У меня возвращено 2 значения: значение статистики теста, и связанное с ним значение p-value, в моем случае получилось 0.011658577248454094. А так как 0.0116 < 0.05, и для отклонения нулевой гипотезы p-value должно быть не выше альфы 0,05, то у нас есть веские доказательства того, что мы отвергаем нулевую гипотезу на уровне значимости 0,05.
Но перед тем, как делать вывод об отсутствии различий, мы еще должны выяснить, была ли мощность использованного статистического критерия достаточной для их обнаружения. А мощность упирается в размер выборки. Нельзя сравнивать близкие законы при малых объёмах выборок.
Меняем Критерий Шапиро-Уилка на тест Андерсона, print (stats.anderson(x)), проверяем еще раз, что данные в выборке более менее нормально распределены. За тестом Андерсона Дарлинга часто используют w^2 Мизеса. Результат можно проверить даже визуально:
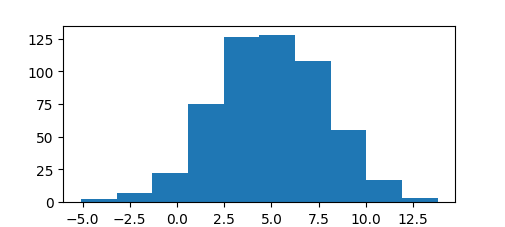
Давайте проведем F-тест, так как настало время проверки статистической значимости различий. Допустим, нужно сравнить работу продажников из двух городов.
Используем для этого ANOVA (дисперсионный анализ) из библиотеки Scipy, командой stats.f_oneway. Нулевая гипотеза ANOVA предполагает, что мат. ожидания совпадают. Если t-критерий Стьюдента используется для сравнения среднего значения в двух независимых или зависимых группах, то f-критерий проверяет, есть ли вообще разница. Можно использовать для большего количества выборок, чем 2. Разумеется, ANOVA не является f-тестом в полной мере, это модель регрессии и считается обобщенной линейной моделью (GLM). ANOVA используется для сравнения среднего значения какого-то признака в независимых группах.
import matplotlib matplotlib.use('TkAgg') import scipy.stats as stats a = [2,3,1,4,3,4,2,4,-1,32,12,53,2,2,3,2.3,2,4.2,3,32,1] b = [3,4,-1,3,4,43,4,14,2.3,1,3,2.3,12,42,2.4,3,4,1,4,1,2] print (stats.f_oneway(a,b)) |
Получаем F-статистику F_onewayResult(statistic=0.0386380063725391, pvalue=0.8451628704190369), что говорит нам, больше ли дисперсия между группами, чем дисперсия внутри групп, и вычисляет вероятность наблюдения этого коэффициента дисперсии, используя F-распределение. Конечно, для научных публикаций данных недостаточно, нет степеней свободы. Но заветный P-value мы получили и теперь знаем, что раз 0.8451628704190369 > 0.05, то работа продажников явно завязана не только на тех данных, что у нас имеются. У нас отказ от нулевой гипотезы, так как данные не выглядят нормально. Нулевая гипотеза a = b, альтернативная a ≠ b. На самом деле, если нет желания разбираться с кучей критериев, достаточно освоить ANOVA и Bootstrap, так как все укладывается в общие линейные модели.
Сравним средние двух выборок с помощью T-test. Для T-test нам нужны среднее выборки, ее размер и отклонение. Мы хотим узнать, есть ли различия в двух группах данных, пусть это будут результаты A/B теста для туториалов в мобильном приложении. Для этого нужно интерпретировать статистическое значение в двустороннем тесте с примерно нормальным распределением, что означает, что нулевая гипотеза может быть отвергнута, когда средние значения двух выборок слишком отличаются. В R мы использовали функцию t.test() для простого t-теста Стьюдента, в Python мы пойдем более комплексным путем. Можно выполнить как односторонний, так и двусторонний T-test в Python. Если у вас много шума в данных, не забудьте сделать дисперсию. Стьюдента для независимых выборок считают с равными дисперсиями. Честно говоря, T-test самый консервативный из всех, ему нужна полная гомогенность выборок (50 на 50), и строго нормальное распределение. Для тестов бинарных или непрерывных метрик не подойдет.
У двустороннего теста и p-value получится в два раза больше, чем у одностороннего, поэтому двусторонний тест имеет более строгие критерии для отклонения нулевой гипотезы. Гипотетически, из двустороннего p-value можно получить одностороннее, но при правильно проведенном тесте не должно возникнуть такой необходимости. При двустороннем тесте мы делим p-value 0.05 на два, и отдаем по 0.025 на положительный и отрицательный концы распределения. При одностороннем тесте весь p-value 0.05 располагается в одном конце распределения. Так как второй конец распределения игнорируется, то есть вероятность ошибки: создав новый туториал, можно протестировать односторонним тестом, лучше ли новый туториал предыдущего. Но информация о том, хуже ли новый туториал предыдущего, будет проигнорирована. Но если новый туториал рассчитан на другую аудиторию и мы точно знаем, что он не может быть хуже, то односторонний тест вам подходит и даст бОльшую точность.
Вводные для следующего примера: нулевая гипотеза что мат. ожидания для двух групп равны, дисперсии равны. Данные представляют финансовые результаты двух разных интернет-магазинов схожей тематики.
import matplotlib matplotlib.use('TkAgg') from scipy import stats a = [742,148,423,424,122,432,-1,232,243,332,213] b = [-1,3,4,2,1,3,2,4,1,2] print (stats.ttest_ind(a,b)) |
Результаты завязаны на проблеме Беренса-Фишера, так как точного решения не существует, но вероятность позволяет нам сделать вывод. Если сделать поправку на то, что при маленькой выборке никак не сгруппированных данных у нас большая дисперсия (проверяем дисперсию командой print(np.var(a)) ), то качество данных можно поставить под сомнение. Если данные не распределены нормально, нужен критерий Манна-Уитни, также известный как Критерий Уилкоксона. Выборка у нас небольшая, поэтому Манна-Уитни вполне подойдет, ранги не будут сильно пересекаться. Запуская Манна-Уитни, мы преобразовываем данные в ранги, строим два распределения рангов и пытаемся узнать разность 50-х квартилей ранговых распределений.
Общее предположение Манна-Уитни что все наблюдения из обеих групп независимы и непрерывны. Про непрерывность есть нюанс: допускается небольшое повторение элементов в выборках. H0 = если мы возьмем по одному случайному элементу из первого и второго распределений, то элемент из первого распределения с вероятностью ≠ 1/2 больше, чем элемент из второго распределения. Для начала задаем некую U-статистику, чье распределение мы знаем при условии, что нулевая гипотеза верна:
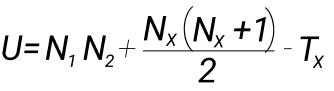
Например, у нас есть две выборки: 1,3,4,6 и 2,7,8. Создаем единый ряд от минимального значения к максимальному: 1,2,3,4,6,7,8. И прописывем ранги, чем ченьше значение, тем меньше ранг. Разбиваем полученный ряд значений по рангам:
| Значение в ряде | Ранг |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 6 | 5 |
| 7 | 6 |
| 8 | 7 |
Считаем сумму значений рангов: T1 = 1+3+4+5 и T2 = 2+6+7. Tx как максимальная это 15 (T2). Nx = это кол-во элементов в выбранной группе с максимальным рангом, то есть 3. Далее проставляем значения в формулу и считаем статистику: U = 4 * 3 + ((2 * (2+1)) / 2) — 15 = 12 + 3 — 15 = 0. Если выборка маленькая, то открываем справочник и смотрим критические значения.
import matplotlib matplotlib.use('TkAgg') from scipy import stats a = [742, 148, 423, 424, 122, 432, -1, 232, 243, 332, 213] b = [-1, 3, 4, 2, 1, 3, 2, 4, 1, 2] u, p_value = stats.mannwhitneyu(a, b) print("two-sample wilcoxon-test", p_value) |
P-value стал 0.0007438622219910575. Сравнивать выборки можно и визуально:
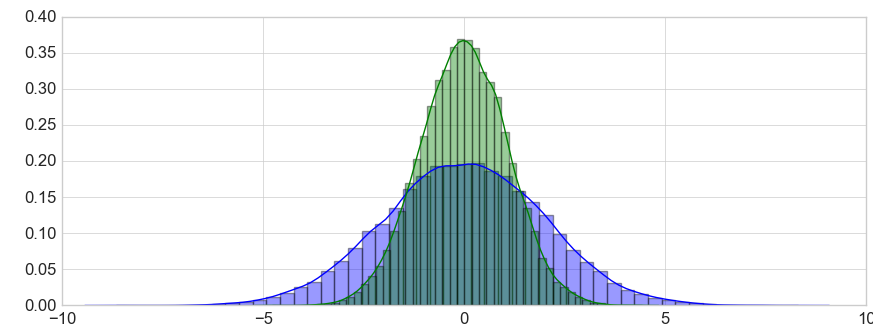
import matplotlib matplotlib.use('TkAgg') import numpy as np from scipy.stats import ttest_ind import matplotlib.pyplot as plt a = np.random.normal(loc=0,scale=24,size=4454) b = np.random.normal(loc=-1,scale=1,size=7643) print(ttest_ind(a,b)) plt.hist(a, bins=24, color='g', alpha=0.75) plt.hist(b, bins=24, color='y', alpha=0.55) plt.show() |
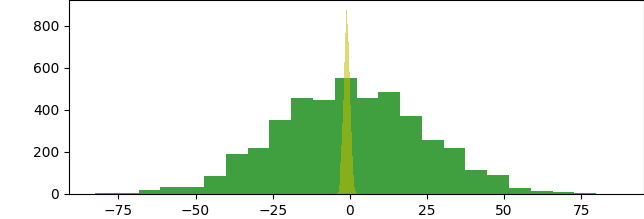
Что намного меньше 0.05, т.е. мы отклоняем нулевую гипотезу критерия Стьюдента про равенство средних. У интернет-магазинов слишком разные данные, нужна сегментация .
Теперь рассмотрим двусторонний тест для нулевой гипотезы о том, что ожидаемое среднее значение одной выборки независимых наблюдений равно среднему значению другой. Аспект «двусторонний» означает, что мы рассматриваем верхнюю и нижнюю границы распределения совокупности данных. Стандартные отклонения должны быть одинаковыми.
import matplotlib matplotlib.use('TkAgg') from scipy import stats from scipy import stats a = stats.norm.rvs(loc = 5,scale = 10,size = 23000) b = stats.norm.rvs(loc = 5,scale = 10,size = 23425) print stats.ttest_ind(a,b) |
Получаем statistic=-0.7043486133916781, pvalue=0.4812192321148787, что намного больше 0,05. А так как р > 0.05 мы считаем маловероятной ошибкой, а р <= 0.05 высоковероятной, то две выборки можно считать равными. Также, для проверки равенства средних подходят Критерий Манна-Уитни, Уилкоксона, Краскера-Уолласа.
Визуализация
Данные важно визуализировать. Не только потому, что заказчики вашей работы — визуалы, есть и более технические особенности. Например, Квартет Энскомба. Это 4 набора точек, у каждой есть X и Y, и по цифрам они идентичны. Но если их визуализировать, то видно, что по показателям выборки из X и Y равны друг другу, а по форме на графике — нет. У всех данных ниже параметры mean=7.50, std=1.94, r=0.82.
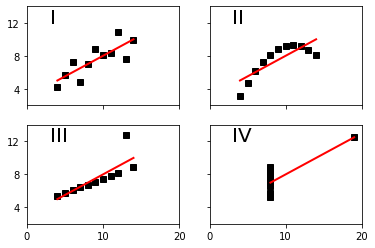
import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import seaborn as sns import pandas as pd import numpy as np sns.set() data = np.random.multivariate_normal([0, 0], [[43, 2], [5, 1.2]],size=25000) data = pd.DataFrame(data, columns=['x', 'y']) for col in 'xy': sns.kdeplot(data[col], bw=.2, shade=False, label="MAU"), plt.show() |
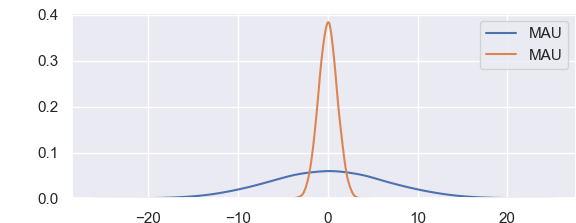
График выше прекрасно подходит для визуального сравнения двух выборок. Доверительный интервал находится между 5 и 95 процентым квантилем, 90% доверительный интервал это двусторонний критерий между 5 и 95.
import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import seaborn as sns import pandas as pd import numpy as np plt.style.use('classic') plt.style.use('seaborn-whitegrid') data = np.random.multivariate_normal([0, 0], [[3.4, 1.87], [2.8, 1.44]],size=25000) data = pd.DataFrame(data, columns=['x', 'y']) sns.distplot(data['x']) sns.distplot(data['y']); plt.show() |
Представленные выше графики достаточно стандартны и вы неоднократно их строили или, по крайней мере, видели. А вот следующий график, Jointplot, уже куда интереснее. Он совмещает в себе гистограммы по x и y, и включает типичный график рассеяния. Получается своеобразный куб из гистограмм.
import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import seaborn as sns import pandas as pd import numpy as np plt.style.use('classic') plt.style.use('seaborn-whitegrid') data = np.random.multivariate_normal([0, 0], [[43, 2], [5, 1.2]],size=25000) data = pd.DataFrame(data, columns=['x', 'y']) with sns.axes_style('white'): sns.jointplot("x", "y", data, kind='kde'); plt.show() |
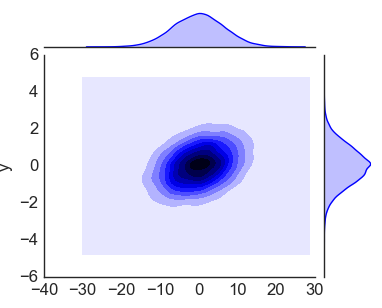
Получилось! Далее построим диаграмму рассеивания.
import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import numpy as np a = np.random.rand(20) b = [3, 4, 3.4, 6, 7, 8, 9, 10, 4, 0.3, 4.2, 4, 23, 3, 33, 3, 1, 4, 0.1, 4.2] colors = np.random.rand(20) plt.scatter(a, b, c=colors, s=100, alpha=0.65, marker=(5, 0)) plt.show() |
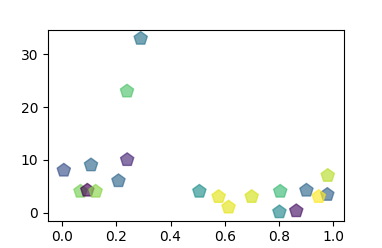
График интересен тем, что полученные рассеивающиеся паттерны позволяют увидеть разные типы корреляции. Стремится с правый верхний угол — хорошая тенденция, расположилось горизонтально — нейтральная тенденция, стремится в левый верхний угол — негативная тенденция.
И Box Plot, куда же без него. Работает с группой из минимум пяти чисел: минимум, первый квартиль, медиана, третий квартиль и максимум. Усы идут от каждого квартиля до минимума или максимума. Всегда можно получить подробную справку по параметрам boxplot, достаточно вбить команду ? sns.boxplot.
import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import seaborn as sns import pandas as pd b = [1, 2, 3, 4, 3.4, 6, 7, 8, 9, 8, 4, 0.3, 4.2, 14, 21, 1, -8] df = pd.DataFrame(b) sns.boxplot(data=df) plt.show() |
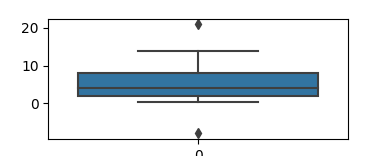
На картинке видно выше, что в наборе данных есть выбросы, в таком случае бывает полезно использовать интерквартильный размах. Это разница между третьим и первым квартилем. Я беру это значение как 1,5 квартиля в обе стороны, от 25-го и 75-го перцентиля. Давайте еще один пример, в котором посмотрим на квартили.
import seaborn as sns sns.boxplot(data["x"]) data["x"].describe() |
count 23.000000 mean 0.112399 std 0.071212 min 0.007407 25% 0.055556 50% 0.103704 75% 0.166667 max 0.244444 Name: x, dtype: float64
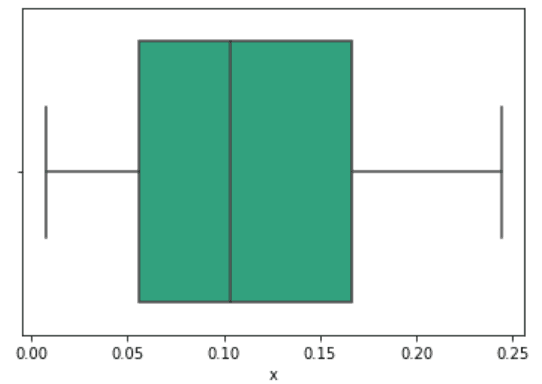
Медиана это 50-ый перцентиль, линия в центре. Данные выше это выгрузка хитов от поведения пользователя, поэтому 50-ый перцентиль это 0,10 кликов. Левая граница большого квадрата это 25-ый перцентиль, значение первого квартиля. И третий квартиль, 75-ый перцентиль. Вертикальные линии по краям показывают статистически значимую выборку.
92 перцентиль отходит от левого края середины графика нормального распределения. Перцентиль это процент, который меньше чем пороговое значение. Узнать вероятность можно и в Excel =NORM.S.INV(0.92), получим результат 1.40507156. Аналогично можно получить перцентиль для левой стороны графика, например, =NORM.S.INV(0.08) и получаем -1.4050716.
А теперь немного 3D, бизнес такое любит:
import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import numpy as np from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D x = np.arange(-2, 5, 0.85) xlen = len(x) y = np.arange(-5, 2, 0.25) ylen = len(y) x, y = np.meshgrid(x, y) r = np.sqrt(x**2 + y**2) z = np.sin(r * 1.3) ax = plt.figure(figsize=(8,6)) ax = ax.add_subplot(1,1,1, projection='3d') ax.plot_surface(x, y, z, cmap=cm.coolwarm, edgecolor='black', linewidth=0.23, antialiased=True) plt.show() |
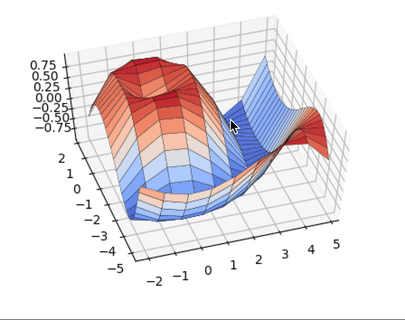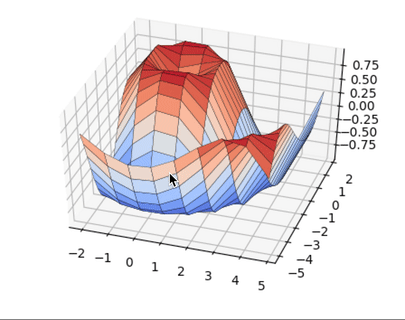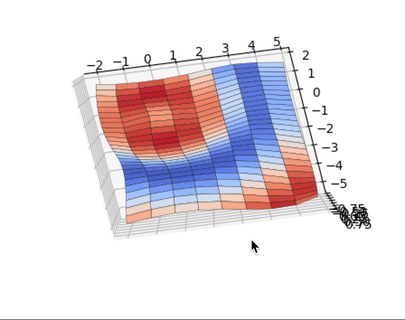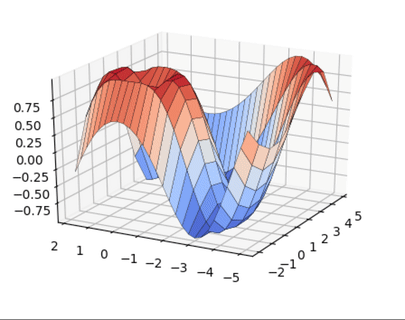
Python Seaborn это лучшее решение для визуализации привлекательных статистических диаграмм. Если же ваша цель это интерактивные графики в вебе, то Python Bokeh, Pygal, Plotly это ваш выбор. Изучайте Python и мат. стат, и ваш продуктовый дизайн сильно вырастет.
Оставить комментарий
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
37 комментариев
Mikhail Neshchadimov
Существует ли специфика анализа данных для финтеха?
Цветков Максим
Банкинг это P&L бизнес, и задачи все идут по теме прибыли и убытков. Надо делить необанки, p2p-платформы (Альфа-поток), сервисы по управлению личными финансами. Общая суть: рынок не зарегулирован, низкие доходы населения, низкая финансовая грамотность. Отсюда Big Data, биометрия, многоканальность.
У финтеха данных много, но данные всегда очень грязные и обрывочные. Но можно партнериться к другими банками для обмена данными (с учетом защиты персональных данных) и телекомами. Это дает некоторые очевидные преимущества: например, чем старше сим-карта клиента, тем больше шанс выдачи кредита.
Задачу для анализа всегда ставит бизнес, и постановка задачи зачастую довольно сложная. Начиная от очевидных хотелок про определение оттока физических лиц (в России банкам очень выгодно, когда у клиента есть дебетовый продукт, на этом банк хорошо зарабатывает), заканчивая психотипированием. Почти наверняка будут задачи про уменьшение универсальности, персонализацию предложения каждому клиенту. Даже в рамках сегмента будут неоптимальные соотношения предложения/ожидания для клиентов на разных концах выборки. Поэтому всегда будут задачи по построению up-sale и cross-sale исходя из соотношения трат на негатив (аренда, коммуналка, штрафы) и позитив (новый гардероб, походы в кино, цирк, горы).
И классика с принятием решения о выдаче кредита. Банки хотят понимать, заплатит ли потенциальный заемщик по кредиту или нет. Это классическая статистика с действием по умолчанию: если не заплатит, то не выдавать кредит (классический банк). Или наоборот, по умолчанию выдавать кредит всем (микро-кредитование). Если нулевая гипотеза что кредит не выдаем, то ошибка первого рода будет выдать кредит и получить клиента, который не платит.
Вторая часть задач про маркетинг в Интернете. Выкатывать рекламу на всех пользователей неэффективно, качество лидов по такой рекламе низкое, у банков будет много отказов на выдачу кредита + неэффективные предложения клиентам, и реклама не окупится. Поэтому огромное внимания уделяется таргетингу. Это классический рекомендательный контент на точках интереса (заправки, ТЦ, аэропорты, университеты), для которого понадобится копить события (JSON), сжимать в батчи и отправлять по https на ваши веб-сервера. Дальше брать ширину и долготу, учесть искажения на полюсах от проекции Меркатора и переходы времени по Гринвичу, «рисовать» гексагон или квадрат для определения области нахождения пользователя. Определять по КЛАДРу, ФИАСу, ISO 3166 или GeoNames, где пользователь находится и что есть вокруг, и после этого вступает в дело рекомендательная система.
Еще всякие леса, вычислительные мощи обычно ограничены, поэтому выгоднее максимально выделить правильные ответы. Например, кредитный скоринг: условие, что отсекаем все заявки от людей, у кого количество просрочек за последние 3 года более трех раз. Таких клиенты падают в отдельную ветку и больше мы на них не тратим ресурсы. Те, у кого меньше трех просрочек, то дополнительно смотрим на зарплату, в скольких банков они обслуживались, и так далее. Можете посмотреть банковский скоринг FICO.
Примерно такие задачи будут первостепенны. Следующий шаг это R, Zeppelin, Presto, Python.
Михаил Боршевитский
Здравствуйте, благодарю за статью. Подскажите по критерию для следующей ситуации: делаю своего рода карточную сортировку на 20 админах, даю список пунктов меню и прошу выбрать те, которые им понятны и нужны в меню. Есть ли способы это подсчитать?
Цветков Максим
Я так понимаю, на выходе у вас бинарные данные 1 или 0 с биномиальным распределением, тогда нужно подсчитать согласованность. Я бы начал с критерия Стюарта-Максвелла, потом Q-критерий Кохрена, и критерий маргинальной однородности. Но только при условии, что у вас связанные выборки (повторное измерение). Точно не тест Стьюдента.
У Q-критерия Кохрана нулевая гипотеза это пропорции «успешных» результатов одинаковы во всех группах. Альтернативная гипотеза это хотя бы одна группа имеет отличия в пропорциях. Нулевая гипотеза отклоняется, когда вычисленное критическое значение Q больше критического значения хи-квадрата. При отклонении нулевой гипотезы выполните парные контрольные Q-тесты Кохрана для выявления отличий.
В зависимости от данных, можно еще обратиться к хи-квадрату Пирсона. Вот простой пример: мы подкидываем монетку 100 раз, и получаем 45 орлов и 55 решек. Ожидаемое 50 на 50, это будет нулевая гипотеза. У хи-квадрата принимается или отклоняется нулевая гипотеза по степеням свободы (df), которые можно подсмотреть в готовых табличках. У нас две стороны монетки, поэтому из 2 мы вычитаем 1 и получаем одну степень свободы. Далее выбираем 0.05 (95%), и получаем по таблице значение 3.841. Далее немного математики, для отклонения нулевой гипотезы нужно получить значение выше 3.841.
Считаем так:
(55 - 50)² / 50 = 25 / 50(45 - 50)² / 50 = 25 / 50
50/50 = 1
у нас одна степень свободы, и полученное значение 1 < 3.841, значит мы принимаем нулевую гипотезу/не может отклонить нулевую гипотезу (кому как удобнее интерпретировать). Попробуем отклонить нулевую гипотезу: монетку подбросили 100 раз, 34 орлов и 66 решек.
(34 - 50)² / 50 = 256 / 50(66 - 50)² / 50 = 256 / 50
512 / 50 = 10.24
10.24 > 3.841, мы отклоняем нулевую гипотезу H0, наши данные статистически значимы.
Andrew Fomichev
Совет подойдет для диапазона значений от 0 до 1? Могу ли с результатом от критерия кохрена понять, достаточной статистической значимостью считать, что в генеральной совокупности переменная распределена по аналогии с моей выборкой?
Цветков Максим
Если известен размер генеральной совокупности, то надо сравнить вашу выборку и имеющуюся выборку из генеральной совокупности. Это Хи-квадрат или точный критерий Фишера. Фишера хорошо с маленькими несбалансированными выборками.
Alexey Sarapulov
Не могли бы привести пример классического процесса проверки а/б теста?
Цветков Максим
Берем данные. У нас есть набор данных с параметрами конверсии до участия дизайнера в проработке лендинга и после, парная выборка. На первый взгляд надо использовать парный t-test, достаточно рассмотреть разность. Но самое первое это проверка на выбросы:
По box-plot видно, что в нашем наборе данных отсутствуют какие-либо существенные выбросы. Следующий шаг это проверка распределения. Для двух зависимых выборок необходимо провести проверку нормальности на различия между двумя наборами данных. Для этого можно использовать гистограмму, Q-Q plot, или статистические тесты.
Видим, что распределение нормальное. Для надежности посмотрим на результаты теста Шапиро-Вилка на нормальность
print (stats.shapiro(df['final_design'])). Получаем W = 0.9910880327224731 и P-value = 0.1491156369447708. Распределение все же нормальное, так как результаты теста незначительные. Если бы распределение было ненормальное, мы перешли бы на тест Вилкоксона.Далее переходим к парному T-test. Его результаты statistic=-8.062787757694716, pvalue=3.5364610751401186e-14. Полученные данные являются статистически значимыми. Можно отвергнуть нулевую гипотезу в поддержку альтернативы. Вмешательство дизайнера в процесс проработки лендинга имело влияние, в данном случае позитивное.
Строгой нормальности обычно не нужно, а тесты для проверки нормальности достаточно строгие. Надо сделать ремарку, T-test’ов много разных.
Alexey Sarapulov
Спасибо, самое простое объяснение, что я видел в рунете)) но, честно говоря, я рассчитывал на ответ про сравнение множества когорот…
Цветков Максим
Тогда вам нужен тест ANOVA (почти как t-test) для проверки данных в целом, поиска аномальных активностей. С t-test у него общего регрессионная модель (GLM). Для доверия результатам теста надо: однородность дисперсии, нормальность данных, равное количество наблюдений в каждой группе и независимость наблюдений. Если кол-во наблюдений в группах значительно разнится, то нужно использовать Kruskal-Wallis H-test или Welch’s ANOVA.
Вот данные. Мы хотим сравнить средние значения 3+ выборок с помощью F-распределения. Будем использовать
stats.f_oneway().Получаем F_onewayResult(statistic=7.3488433965696975, pvalue=0.000674137267723654). В качестве альтернативы можно было использовать fligner-killeen test, он даже лучше.
P < 0,05. А если р < 0,05, то мы считаем, что можно отвергнуть нулевую гипотезу. Нулевая гипотеза (H0) состоит в том, что нет разницы между группами, а альтернативная гипотеза (H1) про наличие различий. Различия есть, и следующая задача это определить, какие группы отличаются друг от друга. Но перед тестом следовало бы поработать с данными, по графикам видно, что есть выбросы.
Если данные распределены ненормально, то смотреть в сторону Dunn’s Test, Краскал-Уоллис. Указываю их вместе, так как критерий Краскала-Уоллиса тождественно равен критерию Манна-Уитни, если у вас две группы для сравнения.
Новичков Игорь
Спасибо! Но ведь надо перед этим проверить данные? именно те что в табличной форме импортированы.
Цветков Максим
Да, надо. Узнать количество строк можно командой
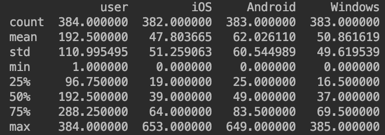
print (len(objects)), количество столбцовprint (objects.shape), типы данныхprint (objects.dtypes).Далее идет описательная статистика, команда print
(objects.describe(include="all")). Получаем описание в рамках порядковой (данные для сравнения), количественной (числа) и номинальной шкале (числа не для сравнения).std это стандартное отклонение (корень из дисперсии), mean это среднее, 50% (медиана) это квантиль, 25% и 50% это квартили. Квантиль это доля случаев меньше определенного значения. Смотрим на данные и ищем аномалии.
Еще нужно смотреть плотность данных, тут поможет гистограмма на примере колонки Windows
Видим выбросы справа. И это критично, как и колокообразная форма (так как наблюдений больше 150). Не критичное это отклонения от симметрии.
Alexey Rekutov
Спасибо, можно уточнить, из чего складывается этот t-test, какой у него принцип, почему я должен ему доверять?
Цветков Максим
Давайте опять на примере: у нас есть зависимые выборки, данные a/b теста до и после теста посадочной страницы. Берем t-критерий Стьюдента, также нужно найти число степеней свободы df, и взять за основу для принятия решения критическое значение t-критерия Стьюдента (0.05) с учетом степеней свободы df. Нулевая гипотеза: средние значения двух выборок равны. Для отклонения этой гипотезы значение t-критерия должно быть равно или больше 0.05, тогда считаем, что можно брать в расчет результаты a/b теста.
Проверяем данные на нормальность:
Данные можно считать нормальными, так как mean и 50% очень похожи. Теперь смотрим на разность каждой пары значений по строкам:
Вычисляем среднее разностей:
Стандартное отклонение разностей от среднего:
И считаем долгожданный t-критерий Стьюдента:
Получаем значение t-критерия Стьюдента = 1,83, которое при числе степеней свободы df 6-1 = 5 и уровне значимости 0,05 надо сравнить со значением из таблицы: 2,57. Полученное значение 1,83 ниже критического 2,57, мы принимаем нулевую гипотезу. Статистически значимых различий до и после проведения теста нет.
И проверим правильность подсчета:
Если же интересует голая теория, то предположим, что хотим сравнить два значения скорости ответа респондентов. И понять, есть ли между ними разница. Это как раз кейс для t-test. У нас есть следующие наборы данных: Resp A: {10.2, 8.9, 12.5, 9.8, 11.3} и Resp B: {12.7, 11.8, 13.2, 10.5, 12.1}.
Первым шагом мы формируем гипотезу: Нулевая гипотеза (H0): ‘Нет существенной разницы в среднем времени отклика между респом A и респом B’.
Альтернативная гипотеза (Ha): ‘Существует значительная разница в среднем времени отклика между респами A и B’. Статистическую значимость возьмем как 0.05 (5%).
Далее по шагам:
Среднее значение для респа A: mA =
(10.2 + 8.9 + 12.5 + 9.8 + 11.3)/5 = 10.54.Среднее значение для респа B:mB =
(12.7 + 11.8 + 13.2 + 10.5 + 12.1)/5 = 12.06.mA-mB = 10.54 – 12.06 = –1.520.
Стандартное отклонение респа А A:sA = 1.394
Стандартное отклонение респа B:sB = 1.026
Размер выборки респа A:nA = 5
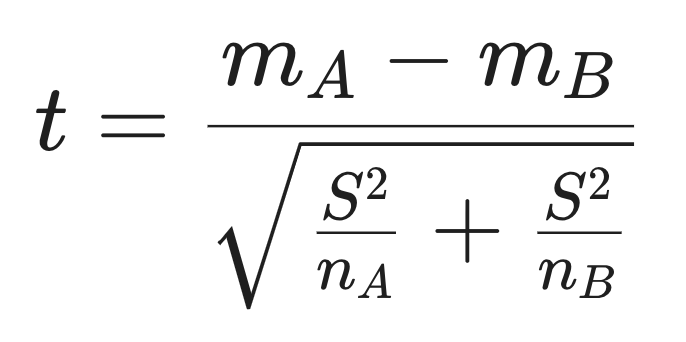
Размер выборки респа B:nB = 5
Формула:
по которой получается
t = (10.54 - 12.06) / Ö((1.394^2 / 5) + (1.026^2 / 5)) = –1.9636.Далее нужно определить T и P-значения. Гуглим таблицу критических значений t-критерия Стьюдента. В нашем случае число степеней свободы равно объему выборки за вычетом числа параметров, которые необходимо вычислить в ходе анализа, т.е.
nA + nB- 2 = 8. Выше мы договорились, что уровень стат. значимости возьмем за 0,05, а число степеней свободы равно 8. t-значение составит примерно 2,306. Двухвыборочное значение p равно 0,0852. Если полученное t-значение попадает в область отклонения или p-значение меньше уровня значимости, то мы опровергаем нулевую гипотезу. У нас рассчитанное t-значение (-1,9636) не превышает критическое значение (2,306), а p-значение 0,0852 больше 0,05. А это значит, что разница между двумя средними значениями не является статистически значимой. В значениях от респа А и респа B разница отсутствует.Marker Frank
Получается что p-value это вероятность правильного решения, но ведь даже ошибка в пяти случаях из ста это могут быть миллионы долларов, или 5 убитых пациентов, неужели все полагаются на 5% допуска ошибки без дополнительных способов проверки?
Цветков Максим
Если полученное значение ниже 0.05 мы отклоняем H0 гипотезу и считаем, что разница является статистически значимой. Но на p-value влияет множество выбросов из данных, поэтому часто используют оценку p-value с помощью bootstrap. И тогда возможна ситуация, когда полученные p-value сильно выше 0.05. Но если провести bootstrap для p-value и оценить его 50 квантиль (медиана), то он может быть равен p<0.05, и можно отклонить нулевую гипотезу. Так часто валидируют эксперименты. Либо взять за правило p-value не 0.05, а 0.01, получается более строгий порог для "отвергнуть основную гипотезу".
При проектировании критически важной инфраструктуры может быть и p-value < 10^-5. Вообще, p-value зависит от числа наблюдений и величины отклонения, и нашей субъективной уверенности. Чем больше элементов в выборке, тем более точный вывод. Чем меньше коэффицент вариаций, тем более точный вывод.
Василий Тиньк
Здравствуйте, у меня есть множество наблюдений в разных группах, по каким принципам принято полученные наблюдения раскидывать по когортам?
Цветков Максим
Когортный анализ больше про определение динамики изменений внутри продукта. Также можно понять, устойчивая ли бизнес-модель. И для сравнения показателей когорт друг с другом, например, LTV клиентов с промо-кодами и без.
Предположим, что наблюдения схожие: тогда можно использовать иерархический кластерный анализ, он как раз разбивает объекты на группы. Кластер это попросту скопление объектов, близких по своим свойствам. Близость свойств между объектами определяют разными алгоритмами, обычно это евклидово расстояние или block. Евклидово позволяет делать большое расстояние гигантским, так как различия возводятся в квадрат. Block не возводит в квадрат, и большие различия получаются менее значимы.
В качестве визуализации подойдет дендрограмма, она позволяет понять, где произошел скачок в расстояниях между кластерами. Возьмем нормированные данные в виде таблицы и импортируем в Python. Каждый цвет обозначает свой кластер, а синие это области, на которых алгоритм решил прекратить объединять в кластеры.
Если подняться на более абстрактный уровень, то обязательно нужно сформировать когорты, выбрать метрику для отслеживания изменений и временную разбивку. Например, первая покупка сделана в определенный день/неделю/месяц, или промокоды, каналы привлечения, наличие подписки. Выбираем метрику (GMV / сколько денег прошло, Profit / прибыль, ARPU), средний чек/ARPPU, возвращаемость, частотность в единицу времени. И с какой гранулярностью времени будем следить за метрикой.
М. Антон
Добрый день. Не могу никак осознать, как понять сколько нужно пользователей для проведения статистически значимого теста.
Цветков Максим
Самый простой и не самый правильный способ: умозрительно прикинуть минимально ожидаемый эффект, взять константы мощности и значимость эксперимента, и дальше веб-сервисы вам скажут нужный объем выборки для теста с распределением 50%/50%.
Допустим, базовая конверсия (с1) = 4%. Лифт, который мы хотим (lift) = 8%. Эти же цифры вводим в калькулятор.
И сразу считаем новую конверсию: 0.04 * (1 + 0.08) = 4.3%
Вот пример для R:
И сразу в цифрами:
Каждый из способов делает аппроксимацию биноминального распределения, поэтому в каждом подходе размер выборки будет немного отличаться. А калькулятор просто занижает нужный размер выборки.
Посложнее: в общем случае это ваша текущая конверсия (до начала теста), ожидаемый рост конверсии (например, экспертно считаем что конверсия должна подскочить на 20%), p-value (вероятность ошибки). При этом почти всегда берут 5% p-value и 80% мощность. Если мощность 0.95 и уровень значимости 0.1, то можно их «перевернуть» и получить мощность 0.9 и уровень значимости 0.5. Уровень значимости показывает вероятность, что нулевая гипотеза верна. То есть significance level, на основе которого мы принимаем или отвергаем гипотезу с полученным p-value.
Za :
p-value 5%
2-sided 1.96
1-sided 1.65
Либо
p-value 1%
2-sided 2.58
1-sided 2.33
Либо
p-value 0.1%
2-sided 3.29
И Z1−β:
Мощность: 80% (Z1−β = 0.84), 85% (Z1−β = 1.04), 90% (Z1−β = 1.28), 95% (Z1−β = 1.64)
Вот одна из формул из моей практики, подразумеваются равные выборки. Сначала считаем дисперсию, текущая конверсия 50%, и ожидаемая 50% + (20% / 2) = 60%.
0.5(1 – 0.5) + 0.6(1 – 0.6) = 0.25 + 0.24 = 0.49.
Теперь берем уровень достоверности 95%, это дает нам значения Za = 1,96.
1. 0.49/0.01 = 49 * 2 = 98
2. (1.96 + 0.8)² = 7.6176
3. Объем выборки = 98 * 7.6176 = 746 (делим на контрольную и тестируемую выборки)
Формула выглядит так:
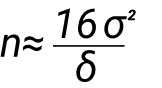
Она не самая лучшая, в числитиле константа 16, в знаменателе нужное нам отклонение. Чем больше значение в знаменателе, тем больше значение в числитиле нам нужно. Например, в знаменателе 1%, это 1/100, в квадрате это 1/10 000, значит нам нужно 10 000 пользователей для проверки улучшения на 1%.
Посмотрите еще мои ответы тут и тут.
Если калькулятор от миллера вас не устраивает, то есть много других: socioline, easycalculation, abtestguide, vwo, есть совсем детские neilpatel. Или через совместное распределение.
Oleg Kovalov
Как посоветуете рассчитывать объем выборки для подтверждения значимости эффекта, если я провожу A/B тест, и надо точно знать, что вариант B будет точно не хуже, чем А?
Цветков Максим
Типичная задача про оптимизацию затрат, где конверсия не будет хуже изначальной. Нужно искать такой размер выборки, при котором мы уверены, что конверсия не упала на заданное число. Это Non-Inferiority A/B Tests.
Либо идти научным путем, тогда это стремящаяся к нулю дельта, и значит и размер выборки стремится к бесконечности. Поэтому прикидываем подходящую дельту: делаем предположение об размере доверительного интервала от размера выборки и решаем, какая точность приемлема.
Diana Sedunova
А вы сами используете калькуляторы? параметр Difference в калькуляторе миллера это мощность?
Цветков Максим
Difference в этих калькуляторах это минимальный эффект, который можно обнаружить.
Мощность теста это шанс ошибиться, допустить ошибку второго рода.
Pavel
>> У меня возвращено 2 значения: статистика хи-квадрата и связанное с ним значение p-value, в моем случае получилось 0.011658577248454094.
Как связана статистика хи-квадрат с тестом Шапиро-Уилка?
>> А так как 0.0116 < 0.05, и для отклонения нулевой гипотезы p-value должно быть не выше альфы 0,05, то у нас есть веские доказательства того, что мы отвергаем нулевую гипотезу на уровне значимости 0,05. Вывод: в первом приближении, отклонений от нормального поведения в транзакциях не выявлено.
Нулевая гипотеза теста H0: X ~ N(mu, sigma). Ваше p-значение получилось меньше альфы, не значит ли это, что нулевая гипотеза отклоняется в пользу альтернативной, что распределение данных существенно отличается от нормального?
Цветков Максим
Как связана статистика хи-квадрат с тестом Шапиро-Уилка?С помощью Шапиро Уилко я отвечаю на вопрос, является ли выборка нормально распределенной. Классика: р-value меньше 0.05, буду использовать непараметрические методы, больше 0.05 — параметрические. P < 0.05 говорит нам о том, что распределение не нормальное. А критерий хи-квадрата помогает понять, являются ли наблюдения в двух группах независимыми друг от друга. Можно в качестве альтернативы взять Краскела-Уоллиса, он тоже про гипотезу сдвига данных (особенно, когда выборок много). По результатам, допустим, можно выбрать t-test для понимания, был ли завод более эффективен в 2020 году чем в 2010 году. Или, если выборки зависимые, то тест Фридмана. И если тест отверг нулевую гипотезу, ищем победителя пост-хок тестом Cohover-Lman.
Нулевая гипотеза теста H0: X ~ N(mu, sigma). Ваше p-значение получилось меньше альфы, не значит ли это, что нулевая гипотеза отклоняется в пользу альтернативной, что распределение данных существенно отличается от нормального?Все верно. Так как полученное p-value меньше критического значения, с вероятностью 95% отклоняем нулевую гипотезу о равенстве средних, это так. Если p-value ≤ α: данные не соответствуют нормальному распределению и мы отклоняем H0. Любой низкой p-value дает нам основания отклонить нулевую гипотезу и считать, что есть разница между тестовой и контрольной группами.
Значение p-value > α: не отклоняем нулевую гипотезу, так как значение p больше, чем уровень значимости. При этом мы не можем сделать вывод, что данные не соответствуют нормальному распределению. И нельзя сделать вывод, что данные соответствуют нормальному распределению.
Но как в анекдоте: есть нюанс. Разные критерии проверяют разные гипотезы (равенство медиан, средних, распределений, дисперсий, …) на одной и той же метрике. Тест проверяет нулевую гипотезу, что наша выборка была извлечена из генеральной совокупности с нормальным распределением. А вот насколько отклонение от нормальности существенно с точки зрения применения параметрики, часто решается исходя из полученных графиков/данных. На выборках небольшого объема, но сильно отличающимся от нормального распределения, мы можем себе позволить р-value больше 0,05, а вот на больших выборках и небольшие отличия будут значимы на уровне р<0,05. Значение p-value не зависит от альфы, а принятие или отклонение Н0 очень даже зависит.
И опять же, я могу использовать критерий Колмогорова-Смирнова, с которым игрушечные выборки будут проходить тест на нормальность, даже если они явно ненормальные и это видно на глаз. И наоборот, на огромных выборках будет отвергнута гипотеза о нормальности данных, хотя на b2c проектах небольшие отклонения от нормальности не являются проблемой. Можно весь вечер играться командой
ks.test(rnorm(n, mean = 0, sd = 1),pnorm)и увеличивать свой скепсис касательно критериев. Ведь чем больше выборка, тем менее значимы отклонения от нормальности в распределении данных. А вот такие тесты нормальности работают наоборот: чем больше данных, тем больше мощность, и тем чаще p-value < 0,05.Kirill V. Nikulin
Здравствуйте, а как по boxplot понять распределение данных? Или он не для этого?
Цветков Максим
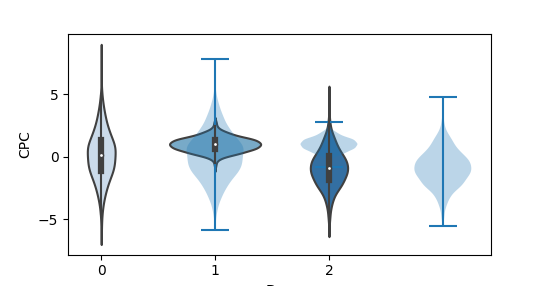
Лучше использовать Violin plot, он нагляднее показывает распределение. По нему проще понять, где сконцентрировано больше данных, вокруг медианы или около максимума/минимума.
Классически идет с черной толстой полосой в центре, которая показывает интервал между четвертями. Эта полоса перетекает в тонкую черную линию, которая визуализирует 95% доверительные интервалы, и белая точка в центре это медиана.
Артём
Максим,подскажите плз, как Вы построили этот график
можно код?
Цветков Максим
Не уверен, что делал эту картинку полностью на Python. Раз я сейчас слету не знаю быстрого способа её повторить, видимо, использовал и другие средства визуализации. Кривоватый левый квантиль косвенно это подтверждает. То, что в предновогоднее время быстро приходит на ум:
import numpy as np
import scipy
import pandas as pd
from scipy.stats import norm
import matplotlib.pyplot as plt
mu = 0
sigma = 1
n_bins = 54
x = np.random.normal(size=1000)
fig, axes = plt.subplots(nrows=2, ncols=1, sharex=False)
median, q1, q3 = np.percentile(x, 50), np.percentile(x, 25), np.percentile(x, 75)
n, bins, patches = axes[1].hist(x, n_bins, normed=True, alpha=.1, edgecolor='black' )
pdf = 1/(sigma*np.sqrt(2*np.pi))*np.exp(-(bins-mu)**2/(2*sigma**2))
bins_1 = bins[(bins >= q1-1.5*(q3-q1)) & (bins <= q1)] bins_2 = bins[(bins <= q3+1.5*(q3-q1)) & (bins >= q3)]
pdf_1 = pdf[:int(len(pdf)/2)]
pdf_2 = pdf[int(len(pdf)/2):]
pdf_1 = pdf_1[(pdf_1 >= norm(mu,sigma).pdf(q1-1.5*(q3-q1))) & (pdf_1 <= norm(mu,sigma).pdf(q1))] pdf_2 = pdf_2[(pdf_2 >= norm(mu,sigma).pdf(q3+1.5*(q3-q1))) & (pdf_2 <= norm(mu,sigma).pdf(q3))] #функция плотности вероятности axes[1].plot(bins, pdf, color='blue', alpha=.6) axes[1].fill_between(bins_1, pdf_1, 0, alpha=.36, color='orange') axes[1].fill_between(bins_2, pdf_2, 0, alpha=.36, color='green') axes[1].set_ylabel('Probability Density') #Ящик с усами axes[0].boxplot(x, 0, 'gD', vert=False) axes[0].axvline(median, color='orange', alpha=.6, linewidth=.5) axes[0].axis('off') plt.show();
Либо не сильно заморачиваться и:
Если бы я писал статью сейчас, то использовал box & beard plot и/или distplot.
Евгений Козлов
Здравствуйте! пока сижу в карантине, решил ваш блог перечитать. В целом, все очень понятно, но ни в одной статье не смог найти, как вычислять квантили?
Цветков Максим
Допустим, правостороняя область, которая от квантиля до бесконечности. Возьмем функцию для стандартного нормального распределения: 1 — α.
Получаем критическую область от 1.959963984 до бесконечности.
Антон Иванов
Здравствуйте, спасибо за статью! Подскажите, пожалуйста, как произвести проверку на нормальность по критериям Хекази-Грина.
Ксения
Максим, спасибо за статью!
Подскажите, пожалуйста, при двустороннем тестировании нужно делать только поправку на уровень значимости (/2) или при расчете в калькуляторе также нужно делить минимально обнаруживаемый эффект также на 2? (Если относительное изменение = 11%, тогда в калькуляторе ставим 5.5?) Или данная поправка не нужна?
Цветков Максим
Для двусторонних t-тестов нужно рассчитывать размер выборки на основе произвольной переменной, называемой минимально обнаруживаемым эффектом (MDE). И тут, как и в любой статистике, зависит от многих факторов.
Официально, делить не надо. Вот пример:
H0: среднее = 20
H1: среднее ≠ 20 (Это то, что мы хотим доказать).
Отклоняем по условию: Z <= - Z2.5 и Z>=Z2.5 (5% / 2).
Если скажем, что среднее значение выборки = 22 и стандартное отклонение 2, то
Z = (22 — 20) / (2/(100²) = 10
Значение не попадает в диапазон -1.96 — 1.96. Деление было только один раз. Если говорить про калькуляторы, то за мощность в них отвечает параметр difference. Для мощности также берем одностороннюю вероятность.
Вообще, минимально обнаруживаемый эффект (MDE) это чем больше размер выборки, тем меньше дисперсия в нашей выборке, и поэтому мы можем обнаружить меньший эффект. Значит, этим параметром можно играться относительно произвольно. И наоборот, при маленьком размере выборки мы можем обнаружить только относительно больший эффект (при прочих равных условиях). Этим двусторонний тест сам по себе и хорош, выручает когда нет глубокого понимания статистики (а его нет почти ни у кого). Я всегда считаю двусторонние вероятности, за исключением только положительных значений. Мощность меньше, зато ЦПТ работает отлично и статистика будет распределена как Стьюдент. Можно и односторонние гипотезы тестировать, делить уровень значимости на 2, это как будто аналог тестирования двусторонних гипотез.
Посмотрите на картинку. Нижняя линия это вероятность, область под стандартным нормальным распределением, которая либо ниже -2,40, либо больше +2,40. Таким образом, вероятность составляет 0.009+0.009 = 0.018, т.е. вероятность 0.009 как в нижнем (левом), так и в верхнем(правом) хвосте. Таким образом мы можем прийти к выводу, например, что у недоспелых арбузов концентрация витамина А меньше, чем у общей популяции.
Любой частотный анализ это α — уровень значимости, β — мощность, n — размер выборки, mde — эффект. Они все взаимосвязаны и считаются заранее, до запуска эксперимента. А после запуска уже можно добивать поправками. Так вот, односторонние и двусторонние критерии отличаются только параметром мощность = α или α/2. А мощность это шанс совершить ошибку второго рода, очень похоже на уровень значимости, но тесно связано с величиной эффекта, сильнее чем уровень значимости.
Поэтому ответ скорее такой: если низкая мощность, то применяем поправки. Это не увеличит вероятность ошибки второго рода, и на такой результат можно ориентироваться. И величину эффекта всегда имеет смысл сделать побольше. Маленький эффект может и не окупить потраченных усилий…
Дмитрий Бойко
Привет! срочный вопрос. Я в этом не очень разбираюсь. У меня на двух т-тестах есть p-value 0.435 и p-value 0.0169. Что тут принимается?
Цветков Максим
Первый — гипотеза о равенстве средних не отвергается.
Второй — отвергается.