Scikit-learn: SVM, линейная регрессия, градиентный спуск
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Warning: WP_Syntax::substituteToken(): Argument #1 ($match) must be passed by reference, value given in /home/users/a/artmax2/domains/your-scorpion.ru/wp-content/plugins/wp-syntax/wp-syntax.php on line 383
Для начала ответ на главный вопрос: а где мне, дизайнеру, пригодится линейная регрессия? Она популярна для решения прикладных задач, вроде прогнозирования. Это в первую очередь таргетированная реклама, нейрон в слоях классификации, простенькие системы скоринга для банков. В общем, любые задачи, где отношения между переменными линейны по своей природе: как возраст влияет на здоровье или сколько операторов в банке справляются с поставленными KPI. Или есть ли связь между продажаи и затратами на таргет, какие площадки больше всего влияют на продажи, линейна ли наблюдаемая зависимость.
В мире ML существует три базовых направления: регрессия для предсказания численных значений, классификация для раскидывания сущностей по неким признакам (кошки/собаки, уволится/не уволится), и кластеризация для группировки похожих объектов лучше, чем rule-based. И обычно есть тестовая выборка для валидации модели и обучающая выборка, в которой заранее известны целевые значения.
Линейная регрессия позволяет прогнозировать зависимость переменной Y на основе переменной X. Визуализируя эту зависимость на графике, получается прямая линия, часто называемая «линия наилучшего соответствия». Линейная регрессия весьма проста, мы прогнозируем Y с учетом X. Есть целевая target-переменная, и потенциальное множество значений для target-переменной бесконечно. Пример: предсказание стоимости квартиры, подавая на вход количество комнат и удаленность от метро, это задача для линейной регрессии. Метрическая модель отвечает на метрическую гипотезу, или целевая переменная линейно зависит от признаков объектов. Типовая задача это прогноз выручки за год магазина, где гипотеза это зависимость количества магазинов и объема выручки. В общем, модель про деньги, поэтому очень популярна в банках: выдавать кредиты надо cумом, каждый параметр влияет на решение о кредите (заработок, дети, просрочки, стаж, состояние здоровья, риск дефолта).
Модели линейной регрессии используются для демонстрации или прогнозирования взаимосвязи между двумя переменными или факторами. Прогнозируемый фактор (фактор, для которого решается уравнение) называется зависимой переменной. Факторы, которые используются для предсказания значения зависимой переменной, называются независимыми переменными. Линейный регрессионный анализ используется для прогнозирования значения переменной на основе значения другой переменной.
Например, стоимость квартиры. Чистим данные, берем модель линейной регрессии и даем задачу: если на вход дать новую квартиру без цены, то модель предскажет стоимость квартиры. И даже скажет, какие параметры влияют на цену.
Линейная регрессия это «строительный блок» для более сложных моделей, например для нейронок. Нейронки это простая череда логистических регрессий, для понимания которых нужна линейная. Она хорошо интерпретируема и её достаточно для многих задач. Существует парная регрессия, это частный случай линейной регрессии, в которой рассматривается только один признак (k = 1). Если все-же признаков больше одного, для аналитического решения может подойти метод наименьших квадратов.
Задача регрессии это минимизация ошибки. По математическому условию, два фактора, участвующие в простом линейном регрессионном анализе, обозначаются x и y. Уравнение, описывающее связь y с x, известно как регрессионная модель. Линейная регрессионная модель также содержит термин ошибки, который представлен Ε или греческой буквой «эпсилон». Термин ошибки используется для учета изменчивости в y, которая не может быть объяснена линейной зависимостью между x и y.
Интереснее работать с категориальными вещественными переменными, но пока что для простоты будем работать только с цифрами. Итак, у нас есть отдел дизайна с 18 дизайнерами, и мы хотим узнать, кто из наших дизайнеров работает наиболее эффективно. Для вычислений будем использовать NumPy. Типичная задача линейной регрессии это определить непрерывную переменную. Если зависимая переменная не непрерывная, тогда это задача классификации, а не регрессии. Я буду рассматривать простые линейные модели, так как обычно хватает простого суммирования значений признаков с некоторыми весами.
Условие задачи: я, как руководитель дизайн-отдела, хочу понять, кто из моих сотрудников самый эффективный. Все работы дизайнеров тестируются по метрике SUM и я точно знаю, у кого какое качество дизайна. Теперь мне надо правильно соотнести количество лет опыта и результативность работы.
В рамках статьи и в рамках терминологии машинного обучения мы будем называть наши наблюдения признаками. Признак это любая характеристика исследуемых данных, выраженная числом. Для начала укажем кол-во лет опыта у специалистов и посмотрим на форму данных командой командой x.shape. У нас всего 18 наблюдений (18 дизайнеров), это один набор признаков. Для добавления второго набора признаков создаем двухмерный массив NumPy. Второй набор данных это результативность (SUM), некий средний балл в диапазоне от 0 до 100. Весь наш набор данных будет называться «признаковым описанием». Внесли данные и визуализировали:
import numpy as np x = np.array([[1,3,4,5,11,0,8,6,3,7,16,0,2,3,2,4,21,4]]) print (x) print (x.shape) y = np.array([[32,54,54,35,86,12,74,67,35,75,94,12,56,54,40,35,87,47]]) print (y) print (y.shape) import matplotlib matplotlib.use('TkAgg') from matplotlib import pyplot as plt plt.scatter(x,y) |
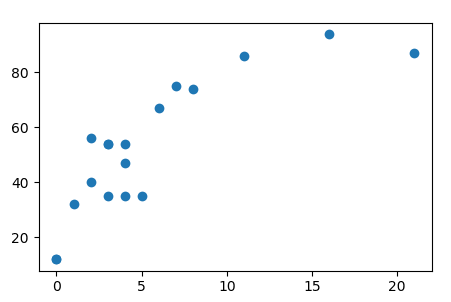
По горизонтали опыт в годах, по вертикали результат SUM. Даже на глаз некая логика в этих данных есть: чем меньше опыта, тем хуже результат работы, по мере увеличения X растет и Y. Сразу возникает желание использовать эти данные об результативности специалиста для прогнозирования, на сколько ему надо повышать зарплату, или уменьшать. Так как начало данных не из 0/0, то нужен интерсепт. Существует понятия сдвига (intercept) и наклона (slope), иногда их называют коэффициентами и параметрами.
Интерсепт это тоже признак, некий сдвиг в данных, пропишем его как x0. Можно использовать и Байеса, у него вполне схожее поведение, но в данном случае он был бы неуместен (не путать с теоремой Байеса). Немного облегчим себе задачу и представим, что у нас нет кривой насыщения, так как у опытных специалистов ранние работы априори плохие, поэтому мы взяли SUM только за последний год. Если человек имеет 0 лет опыта работы, то мы взяли данные за несколько месяцев.
Так как у нас линейная регрессия, попробуем на глаз подобрать вес для признака и интерсепт, и нарисовать по ним линию. Интерсепт может быть 15, а какой наклон? Наклон сложно определить из-за разного масштаба по горизонтали и вертикали. Но попробуем на глаз 3, 4, 5:
import numpy as np import matplotlib matplotlib.use('TkAgg') from matplotlib import pyplot as plt y = np.array([[32, 54, 54, 35, 86, 12, 74, 67, 35, 75, 94, 12, 56, 54, 40, 35, 87, 47]]) print(y) print(y.shape) X = np.array([[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],[1,3,4,5,11,0,8,6,3,7,16,0,2,3,2,4,21,4]]) plt.scatter(X[1], y) plt.plot(X[1], 15*np.ones(18) + X[1]*4) plt.show() |
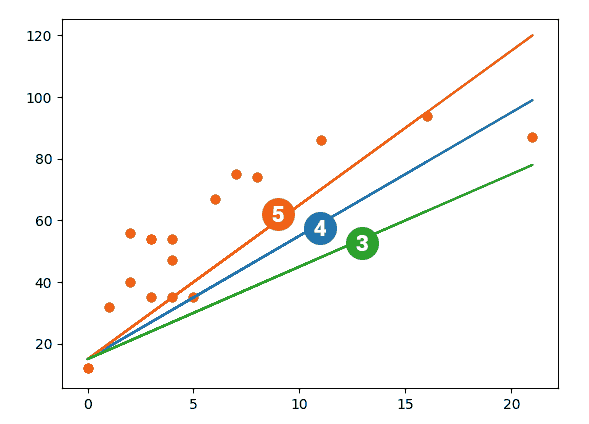
Как это считывать: линия регрессии может показывать положительную линейную зависимость, отрицательную линейную зависимость или не показывать никакой связи. Если линия не наклонная, связь между двумя переменными отсутствует. Если линия регрессии идет вверх, мы имеем положительную линейную зависимость. Если линия регрессии наклоняется вниз, имеется отрицательная линейная зависимость. При этом линия стремится выше предела в 100, это решается клипированием. Более того, правильно клипировать и отрицательные значения. Если применять деревья, то там тоже значения могут выскакивать за пределы возможных, но это целиком зависит от алгоритма.
Допустим, я думаю что значение 5 наиболее близко к реальности. Теперь посмотрим на ошибки, ведь чем меньше ошибка, тем качественнее модель. Ошибки могут быть разные, сейчас мы подсчитаем наши предсказания, возьмем ошибку и просуммируем для каждого наблюдения. Подход весьма примитивен, но это хорошая демонстрация.
y_pred1 = 15*np.ones(18) + X[1]*4 print (y_pred1) err = np.sum(y - y_pred1) print (err) |
Получаем число 179. И это весьма большое значение, значит, мы слишком мало предсказывали. Отрицательное значение значило бы перепрогноз, это более желанный результат. Лучше переработать, чем недоработать. Сейчас же мы можем ошибиться в сторону недопрогноза, и бизнес это не устроит. Есть еще один значимый недостаток: средняя ошибка равна нулю, она плоха тем, что мы можем иметь 2 наблюдения, которые отклоняются в разные стороны на одинаковое число, и при подсчете суммы они обнулятся (-1 +1 = 0). Такие противоположные объекты с одинаковым признаковым описанием скажут нам, что наша модель очень качественная. Хотя в модели могут быть сильные отклонения. Поэтому все разности приводятся к одному знаку с помощью модуля (ошибка MAE), либо все возводится в квадрат, это убирает знак минус. MAE это метод оценки параметров модели. В MAE модули не сильно увеличивают отклонения, считающиеся выбросами. Такая оценка будет более робастная и похожая на медиану, чем MSE. Существуют более сложные метрики, MAPE, RMSPE, и моя любимая RMSE.
Итак, регрессия это целевая переменная, например, потенциальная выручка магазина. И нам надо правильно выбрать функци потерь. MSE это квадратичная функция потерь, считаем матрицу Гессе и понимаем, что она удовлетворяет достаточному условию минимума. Но сейчас мы посмотрим на MAE, так как она дифференцируема,
def calc_mse(y, y_pred): err = np.mean((y - y_pred) ** 2) return err print (calc_mse (y, y_pred1)) def calc_mae(y, y_pred): err = np.mean(np.abs(y - y_pred)) return err print (calc_mae(y, y_pred1)) |
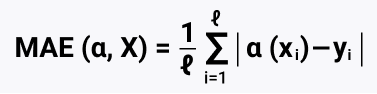
Функции и формула для подсчета выше, принцип подсчета MAE следующий: np.sum(np.abs(y - y_pred1)) / 18, получаем 14.944444444444445. Тут остановлюсь чуть подробнее, MAE (Mean Absolute Error) это среднее абсолютное отклонение (mean absolute error = MAE), такой модуль отклонения устойчив к выбросам. Однако функция модуля не имеет производной в нуле, и её оптимизация может вызывать трудности. Поэтому для измерения отклонения можно просто посчитать квадрат разности.
И тут мы плавно переходим к среднеквадратичному отклонению (mean squared error, MSE), или квадратичная ошибка MSE: np.mean((y - y_pred1) **2), среднее берем вместо суммы, не будем усложнять расчет. Суть метода: минимизация суммы квадратов отклонений фактических значений от расчётных. Применяем, когда намн ужно решить задачу регрессии. Полученную сумму делим на число наблюдений, и получаем MSE. MSE лучше показывает ошибки, чем MAE. Итак, MSE = 326.1666666666667 и MAE = 14.944444444444445. По этим двум точкам строится линия, значит, эта модель (она же линия) будет работать лучше для точек на графике. И именно поэтому регрессия у нас линейная, т.к. ровная линия, которая точнее всего описывает зависимость в данных.
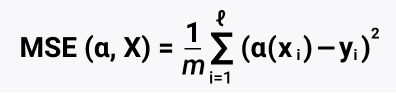
Это был способ на глазок, но куда приятнее автоматизировать процесс. Ведь новые показания SUM приходят каждый месяц и хочется отслеживать рост молодых дизайнеров и актуальность опытных специалистов. Нам нужна формула для автоматического подсчета двух коэффициентов, тут придет на выручку метод наименьших квадратов (МНК). Для работы понадобится матрица, которая по горизонтали и вертикали будет равняться количеству признаков и по форме будет квадратная (18×18). Если у нас 18 столбцов и 18 строк, то эти две матрицы можно перемножать. Итоговая матрица берется по количеству признаков, 2×2.
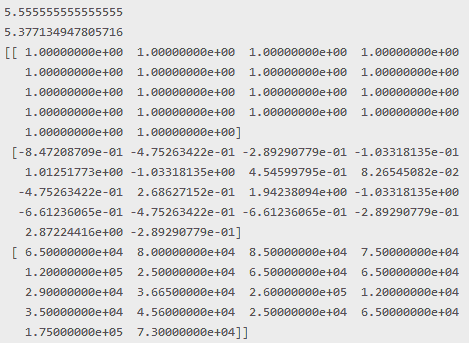
Вводим команду X.shape, узнаем, что у нас матрица (2, 18) . А команда X.T.shape говорит нам, что матрица (18, 2). Значит, эти две матрицы можно перемножать. Командой np.dot(X, X.T) получаем матрицу 2×2 по количеству признаков: [[ 18 100][ 100 1076]].
Надо отметить, что работа с матрицами алгоритмом МНК не очень стабильна. Что имеется ввиду: если определитель матрицы близок к нулю, но корректно вычислить обратную матрицу сложно. Если делить на небольшое занчение, то результатом будет большое значение (10 000 / 0,003 = 3 333 333), и столь малое изменение знаменателя влеук за собой огромные изменения результата. У нас есть 0,003 и 0,0000003, между этими значениями отличие небольшое, они оба очень близки к нулю. Но если разделить 1 на 0,003 и 1 на 0,0000003, то результаты будут 333 и 3 333 333 соответственно, и это уже очень широкий диапазон между значениями. Поэтому обратная матрица неустойчива, минимальная ошибка в определителе влечет огромную ошибку в вычислении обратной матрицы.
Следующим шагом находим из квадртаной матрицы обратную матрицу print (np.linalg.inv(np.dot(X, X.T))), результат [[ 0.11485909 -0.01067464] [-0.01067464 0.00192143]].
W = np.linalg.inv(np.dot(X, X.T)) @ X @ y.T print (W) |
И последний шаг, умножаем на транспонированную матрицу и умножаем на y. И мы получаем набор весов. Это два числа, которые ранее мы пытались угадать на глаз, в этот раз их угадала система:[[32.48548249] [ 3.64261315]]. Мы же предположили, что интерсепт 35 и 5. На практике я бы применил частные производные для вывода формулы, но в рамках нашего примера сойдет и метод наименьших квадратов.
В регрессионном анализе зависимые переменные проиллюстрированы на вертикальной оси Y, а независимые переменные на горизонтальной оси x. Эти обозначения образуют уравнение для линии, которая определяется методом наименьших квадратов. Это важно понимать для прогнозирования поведения зависимых переменных.
X = np.array([[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],[1,3,4,5,11,0,8,6,3,7,16,0,2,3,2,4,21,4]]) y = np.array([[32,54,54,35,86,12,74,67,35,75,94,12,56,54,40,35,87,47]]) print (X.shape) print (X.T.shape) print (np.dot(X, X.T)) print (np.linalg.inv(np.dot(X, X.T))) W = np.linalg.inv(np.dot(X, X.T)) @ X @ y.T print (W) plt.scatter(X[1], y) plt.plot(X[1], 15*np.ones(18) + X[1]*4) plt.plot(X[1], W[0] + W[1] * X[1]) plt.show() |
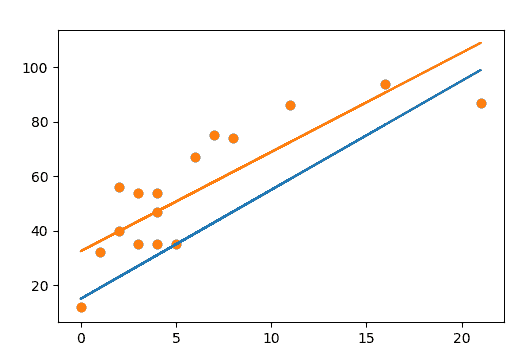
На примере выше видно, что построенная машиной линейная регрессия более жестко отсеивает людей, чем сделал бы это я «на глаз». Это элементарный пример использования машинного обучения для решения бизнес-задач. Теперь подсчитаем новые MAE и MSE для свеженайденных значений:
y_ml=W[0] + W[1] * X[1] print (calc_mse (y, y_ml)) print (calc_mae(y, y_ml)) |
Ранее MSE = 326.1666666666667 и MAE = 14.944444444444445, сейчас MSE = 174.00144700635732 и MAE = 11.478128854730052. Уже куда лучше (помним, чем значение ближе к нулю, тем лучше).
Помимо MSE и MAE, есть логарифмическая функция потерь MSLE и MAPE как средняя средняя абсолютная ошибка в процентах.
Конкретно в нашем отделе есть минимум 6 дизайнеров, которые работают хуже, чем их коллеги с аналогичным опытом. Но в общем то гипотеза подтвердилась: чем больше опыта у дизайнера, тем лучше результат. Но это мы знаем как люди, а для машины эта логика неизвестна, и она теперь точнее нас предскажет итоговый потенциальный прогресс специалиста. Мы даже можем индексировать оклад за рост и результативность специалиста, модель нам позволяет понять, насколько джун растет в сравнении с опытом сеньером. Разумеется, точного предсказания от модели не добиться, ведь рост специалиста зависит от него самого.
Итак, метод наименьших квадратов считает хорошо, и главное, он делает это быстро. Но постоянно его применять не получится, альтернатива: вместо метода наименьших квадратов (МНК) часто применяется градиентный спуск. Градиент это итеративный метод. Он показывает направление наискорейшего возрастания функции. Есть и обратная история: антиградиент, он показывает наибольшее убывание. У МНК есть проблема: он плох при большой размерности X, а точнее, когда много данных. Градиентный спуск не уступает по точности МНК. Принцип его работы простой, сначала он находит плохое решение, потом лучше, еще лучше, еще лучше, и так до наименьшего значения ошибки. Правило: много данных = градиентный спуск. В современном мире выбор алгоритма сильно завязан на производительность, МНК сразу оценивает весь объем данных, а стохастический градиентный спуск позволяет подавать данные батчами. Это помогает экономить оперативную память, которой всегда не хватает. Хотя и МНК, и градиентный спуск легко превращают любую железку в обогреватель. А стохастический градиентный спуск (SGD) нужен когда данные не помещаются в оперативку, и данные нужно разбивать. Это позволяет быстрее достичь глобального минимума, так как в итерациях будет участвовать не весь набор данных. Очевидный недостаток это не попадание в настоящую точку минимума, но в общем то, уровень точности приемлемый. Все по аналогии с веб-аналитикой: есть семплирование, есть и проблемы.
Давайте пощупаем в деле градиентный спуск. Он перебирает разные варианты, и двигается к поставленной цели. Матрицы позволяют сразу выполнять много операций. В математическом анализе есть тема поиска частных производных итеративным перебором весов в MSE. Этим и займемся. У нас одна переменная, но мы добавили инетрсепт и это вес для псевдо-переменных. Получается два признака: инсерсепт и вес признака опыта. Классический градиентный спуск применяется редко, чаще выбирают стохастическую оптимизацию.
Процесс минимизации ошибки в градиентном спуске строится на трехмерном пространстве, образованного за счет двух значений весов (W0 = интерсепт и slope(m) опыт). Мы можем задать начальные веса -1 и 1. Найдем производную для каждого веса векторным способом: где W[0] одновременно и интерсепт и вес. Это вес при псевдо-признаке 1.
import numpy as np X = np.array( [[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 3, 4, 5, 11, 0, 8, 6, 3, 7, 16, 0, 2, 3, 2, 4, 21, 4]]) y = np.array([[32, 54, 54, 35, 86, 12, 74, 67, 35, 75, 94, 12, 56, 54, 40, 35, 87, 47]]) W = np.linalg.inv(np.dot(X, X.T)) @ X @ y.T W = np.array([1, 0.75]) gradient_form_direct = 1/18 * 2 * np.sum(X[0] * W[0] - y[0]) print(gradient_form_direct) |
Мы получаем значение -103.44 , и это не очень хорошо. С таким огромным шагом мы можем просто проскочить нужное нам минимальное значение. Для уменьшения длины шага, мы с каждой итерацией меняем альфу, например, делим на номер итерации. Давайте добавим альфу как скорость обучения, введя alpha = 1e-5 (10 в -5 степени, или 1/10^5). Если видим минус в степени, то отсчет нулей идет назад = — 0,00001.
Значения могут сильно различаться, но после стандартизации/нормализации веса будут предсказуемы: 1,2,10, но точно не 1000. Напомню, W[0] это и интерсепт, и вес одновременно. Вес при псевдо-признаке 1.
alpha = 1e-5 gradient_form_direct = alpha * (1/18 * 2 * np.sum(X[0] * W[0] - y[0])) print(gradient_form_direct) print(W[0] - gradient_form_direct) |
Получили 1.001, с этим уже можно работать. Теперь надо указать минимальное значение, и если ошибка приблизилась к нему, то останавливаем алгоритм. Это называется доходимость. Или ручками задаем фиксированное количество шагов, пожалуй, так мы сейчас и поступим. Есть еще нюанс, что при малом количестве данных мы сделаем больше вычислений, чем сделали бы при МНК, но давайте симулировать ситуацию с большими данными на игрушечных данных:
import numpy as np X = np.array( [[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 3, 4, 5, 11, 0, 8, 6, 3, 7, 16, 0, 2, 3, 2, 4, 21, 4]]) y = np.array([32, 54, 54, 35, 86, 12, 74, 67, 35, 75, 94, 12, 56, 54, 40, 35, 87, 47]) W = np.array([1, 0.5]) gradient_form_direct = 1e-4 * (1/18 * 2 * np.sum(X[0] * W[0] - y[0])) print(gradient_form_direct) print(W[0] - gradient_form_direct) for i in range(2000): gradient_form = np.dot(W, X) W -= (1e-2 * (1/18 * 2 * np.dot((gradient_form - y), X.T))) if i % 200 == 0: print(i, W) |
Отмечу, что у градиентного спуска решение приблизительное. После каждой новой итерации значения искомых весов все ближе и ближе к нужным, но влияет шум и значения никогда не станут идеальными. Если аналитического решения не существует, то градиентный спуск не дойдет даже до удовлетворительных значений.
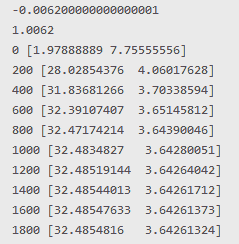
Получаем 32.4854816 и 3.64261324. В практических задачах обычно никто не стремится доказать существование глобального минимума. MSE или log loss ограничены снизу нулём, и чем ближе к нулю, тем больше «ок, сойдет». Просто доказать существование глобального минимума то можно, а достигнуть его куда сложнее. Для особо пытливых умов можно взять альтернативу градиентному спуску, это K-FAC. Или увеличить коэффициент альфа и тогда будет нужно меньше итераций, например 1e-2 и увеличить количество итераций. Так мы дойдем до тех же значений, что мы получили мне помощи МНК. Зачастую используют сразу несколько градиентных спусков, они сходятся к разным точкам, находят разные лучшие начальные приближения, так удается найти лучшую точку минимума. Градиентный спуск имеет линейную скорость сходимости, это вариант более честный. Стохастический — сублинейную скорость, это позволяет не очень долго считать, вопрос мощностей для расчета и количества данных.
Раз уж мы затронули тему масштабирования признаков, давайте разберем пару примеров нормализации и стандартизации. Линейные модели обучения эффективны только на признаках, которые имеют одинаковый масштаб. Поэтому масштабирование признаков это неотъемлемая часть подготовки данных перед применением методов машинного обучения. Нормализация нужна для измерительных признаков, вроде роста или размера зарплаты, стандартизация лучше подойдет для моделей, опирающихся на распределение. В любом случае, стандартизация и нормализация не навредят, все остальное очень индивидуально.
Добавим новый фактор — месячную зарплату.
X = np.array( [[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 3, 4, 5, 11, 0, 8, 6, 3, 7, 16, 0, 2, 3, 2, 4, 21, 4], [65000, 80000, 85000, 75000, 120000, 25000, 65000, 65000, 29000, 36650, 260000, 12000, 35000, 45600, 25000, 65000, 175000, 73000]]) |
Нормализация это диапазон от 0 до 1, с сохранением линейности. Далее принцип нормализации: отнимаем от значения признака его минимальное значение, тем самым признак становится равен нулю, а максимальный признак равен размаху между максимумом и минимумом. Делим на размах и получаем отмасштабированный признак. Другие популярные методы нормализации это квадратный корень, логарифмирование.
Гипотеза простая — чем больше платим человеку, тем лучшего результата работы мы от него ожидаем. Все признаки разномасштабные. Коэффициенты зависят от масштаба, и по коэффициентам мы не поймем значимость признаков при разном масштабе + не все алгоритмы это смогут обработать. Данные нужно нормализировать (интервал 0 до 1), после этого по весам регрессии можно будет судить, насколько важны признаки. При этом форма даных не будет изменена, просто поменяются среднее и дисперсия. Находим для каждого признака минимум и максимум: print (X[1].min(), X[1].max()), print (X[2].min(), X[2].max()). Получаем 0-21 и 12000-260000.
Нормализация по шагам: (X[1].max() -X [1].min()) получаем размах, максимальный опыт у дизайнеров 21 год. Смотрим на минимальный опыт (X[1] -X [1].min()), получаем [ 1 3 4 5 11 0 8 6 3 7 16 0 2 3 2 4 21 4], минимальный опыт ноль. И приводим все к нужному нам диапазону (X[1] - X[1].min()) / (X[1].max() -X[1].min()), результат вида [0.04761905 0.14285714 0.19047619 0.23809524 0.52380952 0. 0.38095238 0.28571429 0.14285714 0.33333333 0.76190476 0. 0.0952381 0.14285714 0.0952381 0.19047619 1. 0.19047619]. Теперь сделаем это для двух признаков:
X_norm = X.copy() X_norm = X_norm.astype(np.float64) X_norm[1] = (X[1] -X[1].min()) / (X[1].max() -X [1].min()) X_norm[2] = (X[2] -X[2].min()) / (X[2].max() -X [2].min()) print(X_norm) |
А теперь стандартизация: мы пытаемся получить стандартное нормальное распределение, это диапазон от -1 до 1 с 0 в середине, и большинство значений скопятся в районе нуля. Так мы сможем привести все признаки к одному масштабу. Это важно для линейных моделей, так как они не смогут работать одновременно с наборами признаков: количество арбузов 100-600, и количество семечек в мандаринах 10000-30000. Также критично для метода ближайших соседей (kNN). Поэтому лучше наши данные заранее привести к виду, когда признаки находятся в примерно одном масштабе.
Смотрим на графики
import matplotlib matplotlib.use('TkAgg') from matplotlib import pyplot as plt plt.hist(X[1], alpha=0.6, color='g') '''либо''' import matplotlib.pyplot as plt plt.hist(X[1], alpha=0.6, color='g') |
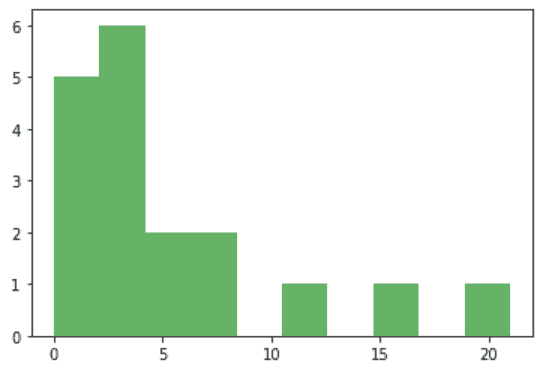
В принципе, похоже на стандартное распределение сотрудников в студиях дизайна: несколько опытных сеньеров-менторов и много джунов/мидлов. Поэтому распределение смещено, это также типичная ситуация для финансовых результатов, так как всегда есть большинство товаров массового потребления и какие-то отложения вправо до бесконечности из-за маленького количества услуг с огромной стоимостью.
Находим среднее по первому признаку X1_mean = X[1].mean(), получаем 5.55. Это средний стаж работы дизайнера. Теперь среднее квадратичное отклонение X1_std = X[1].std(),
X1_mean = X[1].mean() print(X1_mean) X1_std = X[1].std() print(X1_std) X_standarted = X.copy().astype(np.float64) X_standarted[1] = (X[1] - X1_mean) / X1_std print(X_standarted) |
Отрицательные значения в результате это то, что меньше среднего. Идеально среднее значение будет равно нулю, подсчитаем его по первому признаку:
def calc_feature_std(x): result = (x - x.mean()) / x.std() return result X_standarted[2] = calc_feature_std(X[2]) print(X_standarted[2]) |
Данные стандартизировались. Алгоритмам проще работать с признаками в стандартизированном виде. На практике специалисты пробуют и стандартизацию, и нормализацию, выбирая наиболее подходящий способ масштабирования данных, аксиомы тут нет.
Python Scikit-learn: Линейная регрессия и SVM
Существует множество полезных технологий, которые помогают мне грамотно планировать работу отдела дизайна. Часть задач по анализу информации я просто делегировал компьютеру. Например, нейронкам можно скормить изображения, тексты, обучить компьютерному зрению, в общем делегировать работу про матрицу с пикселями. Градиентный бустинг рассчитан на работу с признаками. И в нем есть все инстурменты для этого: свертки, пуллинг. Градиентный бустинг весьма хорош при работе с деревьями.
Но сегодняшняя наша тема это машинное обучение, оно бывает с учителем и без учителя. Обучение с учителем (supervised learning) это про предсказание некой величины. Учитель это база данных, состоящая из пар объект – ответ. Обучению с учителем требуется два набора данных для прогноза: тренировочный и тестовый датасеты. То есть нужен набор данных с готовым правильным ответом, и на его основе будет строиться модель для предсказания ответа при работе со схожими данными. Начнем с простого. А именно с линейной регрессии. Используется для предсказания непрерывной величины, в нашем случае это будет прогноз затрат на услуги фрилансеров. Линейная регрессия по сути нечто вроде алгоритма, который находит в данных паттерн определенного вида между независимой переменной (X) и зависимой переменной (y).
Модель линейной регрессии по объекту x=(x1,…,xn) предсказывает значение целевой переменной, используя линейную функцию. Она строит модель на трейне (тренировочный датасет) и делает предсказание на тесте, возвращая среднеквадратичную ошибку. Итак, модель = linear regression, и есть список признаков.
Возьмем Scikit-learn, в нем есть почти все нужные алгоритмы машинного обучения. Хочу отметить, что я осознанно буду приводить примеры кода, написанные не эталонно, но более простые для понимания и изучения. Дизайнер (а это блог для дизайнеров) вполне может писать код не по всем канонам программирования. Нам главное — решить задачу. Итак, создадим наш набор данных:
import numpy as np import matplotlib as mpl import matplotlib.pyplot as plt import pandas as pd def generate_dataset(n): x = [] y = [] random_x1 = np.random.rand() random_x2 = np.random.rand() random_x3 = np.random.rand() random_x4 = np.random.rand() random_x5 = np.random.rand() random_x6 = np.random.rand() random_x7 = np.random.rand() for i in range(n): x0 = i + np.random.rand() / 0.215 * 3.237 x1 = i + np.random.rand() / 0.211 * 0.698 x2 = i/2 + np.random.rand() - 1024 * 0.002 * 0.02 * 0.05 x3 = i * 0.12 + np.random.rand() * 0.054 x4 = i/1.42 + np.random.rand() x5 = i + 1 * 12 + np.random.rand() * 0.25 x6 = i/4 + np.random.rand() x7 = i + np.random.rand() x.append([x0, x1, x2, x3, x4, x5, x6, x7]) y.append(random_x1 * x1 + 1 + random_x2 * x2 + 1 + random_x3 * x3 + 1 + random_x4 * x4 + 1 + random_x5 * x5 + random_x6 * x6 + + random_x7 * x7) return np.array(x), np.array(y) x, y = generate_dataset(3000) X = pd.DataFrame(x) y = pd.DataFrame(y) X.columns = ['UI', 'UX', 'Payment', 'MRPPU', 'CPA', 'ARPPU', 'Tools', 'TSDB'] y.columns = ['Price_for_freelancers'] |
В примере выше мы вывели в таблицу X признаки, а в таблицу y целевые значения: Price_for_freelancers это величина, которую мы хотим предсказать, то есть цена на фрилансеров.
Обратите внимание на параметр test_size, он позволяет запланировать процент данных, который мы хотим отдать под тест. Если подать параметру число в диапазоне 0-1 (test_size=0.2), то это количество тестовых объектов в процентах. И это самый частотный вариант, но можно подать параметру число больше 1, и это будет фиксированное число объектов в тестовой выборке.
Как было сказано, для построения модели требуется две выборки: первая тренировочная, на ней обучается модель, и вторая тестовая, на которой проверяем, насколько хорошо модель работает. Тест проходит простой сверкой значение цены с предсказанными ценами на услуги фрилансеров. Напомню, в нашем случае признаки записаны в датафрэйм X, и данные о целевой переменной в y. Гипотеза: между X и y должна быть линейная зависимость.
import seaborn as sns new_df = pd.concat([y.reset_index(drop=True), X.reset_index(drop=True)], axis=1) print(new_df) sns.set_style('whitegrid') sns.lmplot('Price_for_freelancers', 'CPA', new_df, palette ='plasma', scatter_kws ={'s':0.4}); |
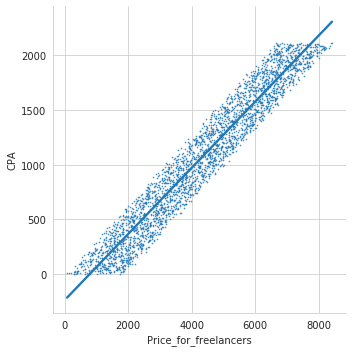
Линия явно проходит через некую зависимость CPA (Cost Per Action) сайтов, нарисованных дизайнерами и Price_for_freelancers (цена за фрилансера). Ситуация искусственная, но очень наглядная. Но помимо CPA, у нас есть множество других признаков. Используем функцию train_test_split, очень популярный способ деления данных на тестовую и проверочную выборку. Выбираем долю данных 0.25, и не будем задавать повторяемость случайного выбора, так интереснее. Получается, что тренировочная выборка 75% и 25% тестовая. random_state не задаем. Начнем строить модель:
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25) from sklearn.linear_model import LinearRegression lr = LinearRegression() lr.fit(X_train, y_train) y_pred = lr.predict(X_test) print(y_pred) |
В примере выше мы вызываем линейную регрессию, обучаем по X_train, y_train, и делаем предсказание по X_test. В результате работы lr.fit мы получаем LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False). И методом predict получаем предсказанные значения.
Но мы же наверняка хотим сопоставить предсказанные и полученные значения, верно?
check_test = pd.DataFrame({ "y_test": y_test["Price_for_freelancers"], "y_pred": y_pred.flatten(), }) check_test.head(10) |
| y_test | y_pred | |
| 2830 | 8853.452885 | 8853.452885 |
| 2988 | 20299.645208 | 20299.645208 |
| 18 | 38.872415 | 38.872415 |
| 1347 | 3825.888260 | 3825.888260 |
| 2838 | 8860.830740 | 8860.830740 |
| … | … | … |
| 1571 | 5212.113755 | 5212.113755 |
| 718 | 1117.374471 | 1117.374471 |
| 2283 | 7192.523583 | 7192.523583 |
| 2646 | 8947.234195 | 8947.234195 |
Тест и предсказание одинаковые. Если визуализировать данные, то все становится примерно понятно:
strangeDataCheck = X.head(8) strangeDataCheck.plot(kind='bar',figsize=(16,10)) plt.grid(which='major', linestyle='-', linewidth='0.5', color='blue') plt.grid(which='minor', linestyle=':', linewidth='0.5', color='red') plt.show() |
Но давайте займемся всякими проверками и узнаем, почему такой странный результат. Существует метрика, которая показывает, насколько сильны отклонения при условии X=Y. Вызываем из класса metrics r2_score, получаем коэффициент детерминации. Не трудно догадаться, что R2 и есть коэффициент детерминации (не путать RSS/TSS и ESS/TSS). Суть такая: целевая переменная описывается суммой 10 случайных, равнозначных и независимых факторов. Допустим, кот может начать мяукать, если показать ему рыку, мясо и еще 8 других продуктов, но мы никогда точно не знаем, мяукнет ли кот. В этом случае метрика R2 = 0. Но если показать мясо утром и рыбу вечером, то кот точно мяукнет, значит R2 = 0,2. Чем ближе к 1, тем лучше. Есть нюанс, что при добавлении в модель новых переменных, которые никакого отношения к объясняемой переменной не имеют, R2 все равно будет меняться в большую сторону. Значение R2 не зависит от масштабов предсказанной величины, и никогда не превышает 1, если мы по ошибке не использовали RSS/TSS (модельные отклонения в числителе, дисперсия данных в знаменателе). Тогда при значении больше 1 считаем, что модель предсказывает не очень хорошо.
from sklearn.metrics import r2_score r2_score(y_test, y_pred) |
В нашем случае коэффицент детерминации = 1, что практически идеально, но невозможно при работе с реальными данными. На реальных данных даже R2 = 0,9 это явное переобучение. Либо, если и тренировочная, и валидационная выборка показывают примерно 0,9, то мы большие молодцы. Но в нашем случае искуственные данные = странный результат.
Небольшое отступление про train/test выборки. Обучающую и тестовую выборку делать одинаковыми нельзя. Никогда. Если так сделать, то цифры с прода вас сильно удивят. Поэтому принято делать выборку на обучающую и тестовую, но здесь тоже есть проблема. Зная все ответы из тестовой выборки, специалисты начинают подгонять модель под эти ответы. Поэтому добавляется третья, валидационная выборка, на которой тестируются финальные метрики. Цифры метрик будут более скромными. Это упрощенная версия подхода cross-validation, когда у разных моделей разные выборки.
Описанное выше это простой метод классификации. Но если мы хотим к классификации добавить еще и регрессию, то тогда нужно использовать случайный лес. В примере ниже разберем алгоритм из деревьев решений под названием случайный лес. Для каждого дерева выбирается подмножество признаков из тестовой выборки, и идет обучение. Каждое дерево дает некий ответ, и если за один ответ проголосовало наибольшее количество деревьев, то этот ответ считается победителем.
Мы ищем коэффициенты W для признаков X, и для тренировки используем метод fit. Записываем результат в отдельную переменную y_pred. После этого создадим объект, который будет нашей исходной моделью.
from sklearn.ensemble import RandomForestRegressor model = RandomForestRegressor(n_estimators=2000, max_depth=18) model.fit(X_train, y_train.values[:, 0]) y_pred_forest = model.predict(X_test) r2_score(y_test, y_pred_forest) |
Алгоритм отработал, методом predict мы можем предсказать цены на фрилансеров и записать их в y_pred в виде простого массива. В переменную y_pred_forest записали предсказанное значение по X_test. В данном случае случайный лес показывает результат хуже, чем логистическая регрессия, 0.714357. Напомню, что я в коде не фиксировал random_state.
И самое сладенькое: посмотрим коэффициенты построенной модели линейной регрессии. Смотрим величину свободного коэффицента W0, он же интерсепт, содержится в атрибуте intercept_. Пишем print(lr.intercept_), получаем значение 3, это коэффицент, подобранный моделью во время обучения. Остальные коэффиценты можно получить командой print(lr.coef_). Мы наглядно видим, насколько каждый параметр модели влияет на результат. Но куда приятнее делать оценку весов признаков визуально.
from matplotlib import pyplot as plt %config inlineBackend.figure_format = 'svg' %matplotlib inline plt.barh(X_train.columns, lr.coef_.flatten()) print(X_train) |
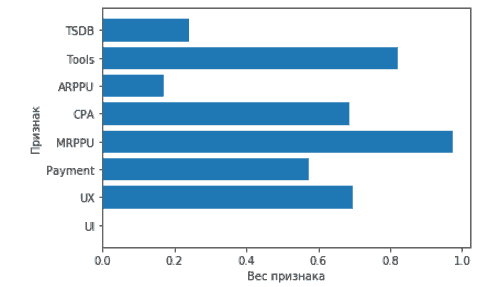
Теперь поговорим про переобучение. Переобучение это когда модель хорошо работает на тех данных, на которых она была построена, но при этом плохо предсказывает на новых данных. Если в наборе мало данных, то шанс столкнуться с этой проблемой весьма велик. Мы не считаем модель хорошей, если не решили проблему переобучения и не подобрали хорошие признаки. Поэтому для уменьшения ошибки надо убирать маловажные признаки, мы для этого используем регуляризацию в лоссе. В библиотеке sklearn линейная регрессия с L1-регуляризацией представлена классом lasso, а L2-регуляризация классом ridge. L1 это модуль, а L2 это работа с квадратом. Можно менять значения альфа, тем самым регулируя величину регуляризации. Правило простое: чем выше альфа, тем сильнее регуляризация, и тем эффективнее мы боремся с переобучением. При использовании регуляризации веса признаков понижают свое абсолютное значение, этим устраняется одна из причин переобучения, а именно бесконтрольный рост коэффицентов. Чем меньше значение альфы в lasso, тем быстрее обнулится значение признака, таким нехитрым образом можно отбирать признаки, когда их очень много. В ridge веса признаков также снижаются по модулю, но более плавно.
Для оценки качества модели регрессии применяются метрики. Вот самые популярные:
Средняя квадратичная ошибка (mean squared error), это средний квадрат разности между реальной и предсказанной величиной. Это MSE, функция ошибок. Считается просто: mse1 = (check_test["error"] ** 2).mean().
Вторая метрика это средняя абсолютная ошибка, отличается от MSE тем, что меньше реагирует на выбросы в данных. Среднее не от квадратов ошибки, а от модулей. Опять же, считается просто: (np.abs(check_test["error"])).mean()
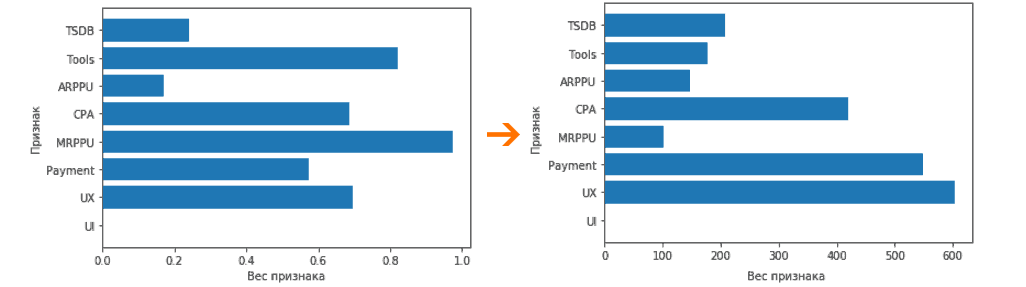
Технически, все это можно было бы сделать и на МНК, но МНК очень затратен по ресурсам при больших объёмах данных. А вот в сторону RMSLE посмотреть вполне можно. Все это здорово, Tools самый доминирующий признак, но почему? Ответ в цифрах:
Признаки имеют разный масштаб?
Работая с линейной моделью, нам требуется для разных признаков разброс значений одного порядка. Достигается это логарифмическим преобразованием + стандартизацией. Простой перевод значения вида 2237.037956 в 0.83846151, это необходимый этап подготовки данных для корректного отбора признаков. В результате у стандартизированного признака среднее значение равно 0, и квадратичное отклонение признака / дисперсия = 1.
sc = StandardScaler() X_train_std = sc.fit_transform(X_train) X_test_std = sc.transform(X_test) |
В примере ниже мы возьмем набор данных, в котором признаки имеют разный масштаб разброса значений. И нужна стандартизация. От значения признака отнимается среднее по данному признаку и делится на среднее квадратичное отклонение.
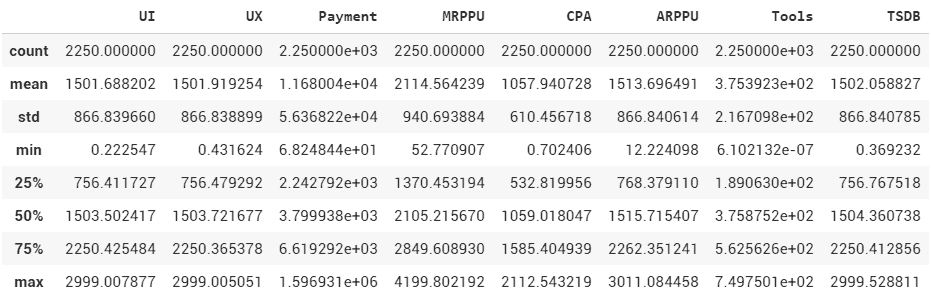
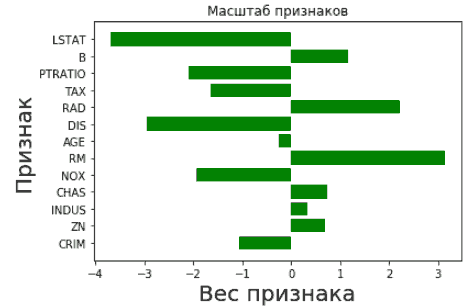
import pandas as pd import numpy as np from sklearn.datasets import load_boston from matplotlib import pyplot as plt %config inlineBackend.figure_format = 'svg' %matplotlib inline boston = load_boston() X = boston.data y = boston.target X = pd.DataFrame(X, columns=boston.feature_names) feature_names = boston['feature_names'] from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42) from sklearn.linear_model import LinearRegression lr = LinearRegression() lr.fit(X_train, y_train) y_pred = lr.predict(X_test) from sklearn.preprocessing import StandardScaler scaler = StandardScaler() X_train_scaled = scaler.fit_transform(X_train) X_train_scaled = pd.DataFrame(X_train_scaled, columns=feature_names) X_test_scaled = scaler.fit_transform(X_test) X_test_scaled = pd.DataFrame(X_test_scaled, columns=feature_names) lr.fit(X_train_scaled, y_train) plt.barh(X_train.columns, lr.coef_.flatten(), color = "green") plt.xlabel('Вес признака', fontsize = 20) plt.ylabel('Признак', fontsize = 20) plt.title("Масштаб признаков") |
fit_transform нам позволяет вычислить среднее значение и среднее квадратичное отклонение из датафрэйма x-Train, и сразу вычислить стандартизированное значение для каждого признака. Далее, как мы уже умеем, берем lr.fit и смотрим новую модель на основе теперь уже стандартизированных признаков. И убираем из модели веса, близкие к нулю.
Возвращаясь к нашему примеру:
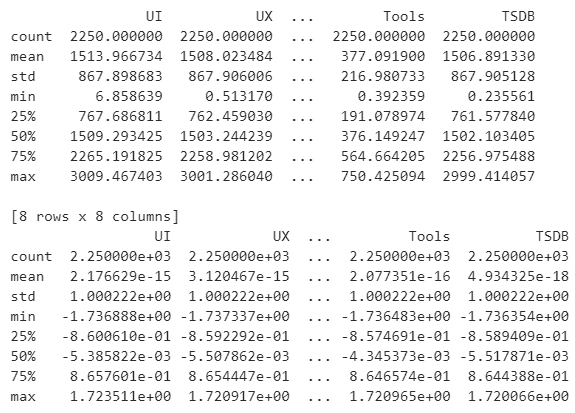
feature_names = ['UI', 'UX', 'Payment', 'MRPPU', 'CPA', 'ARPPU', 'Tools', 'TSDB'] from sklearn.preprocessing import StandardScaler scaler = StandardScaler() X_train_scaled = scaler.fit_transform(X_train) X_train_scaled = pd.DataFrame(X_train_scaled, columns=feature_names) X_test_scaled = scaler.fit_transform(X_test) X_test_scaled = pd.DataFrame(X_test_scaled, columns=feature_names) lr.fit(X_train_scaled, y_train) from matplotlib import pyplot as plt %config inlineBackend.figure_format = 'svg' %matplotlib inline plt.barh(X_train_scaled.columns, lr.coef_.flatten()) plt.xlabel('вес признака') plt.ylabel('признак') print(X_train.describe()) print(X_train_scaled.describe()) |
Support Vector Machine
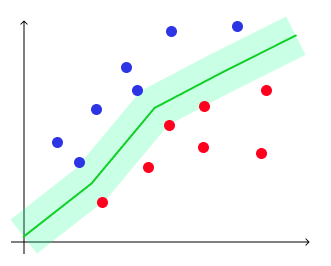
Еще один популярный метод машинного обучения это метод опорных векторов, он же Support Vector Machine (SVM). Состоит из несколько алгоритмов, позволяет решать задачи классификации и регрессии. Например, классификация спама или отсеивание определенного типа выбросов. Визуально это график с линией, причем зазор между объектами и линией максимальный, а ошибка минимальна. Пунктирные линии это степень уверенности алгоритма.
Датасеты для экспериментов можно взять любые из интернета, например archive.ics.uci.edu. Но я возьму свой датасет с данными по дизайнерам: скачать.
Как всегда, несколько нюансов: алгоритмы SVM требовательны к данным, их надо стандартизировать и нормализовывать. Если вы скачали датасет из интернета, то обязательно отмасштабируйте признаки. Чуть выше в статье я показал, как делать стандартизацию (вычитание из признаков их среднего значения, и деление на среднее квадратическое отклонение). Еще можно применить нормализацию: минимальное значение каждого отдельного признака должно быть равным 0, а максимальное 1. В моем наборе данных все это учтено. Давайте начнем:
from sklearn.svm import SVC import pandas as pd data = pd.read_csv("export_dataframe_copy.csv", index_col="Good_UX") data.head() target = "Awards" y = data[target] X = data.drop(target, axis=1) print(y) print(X) |
MinMaxScaler и StandardScaler. StandardScaler вроде как чаще встречается в реальных задачах, и не сохраняет разреженность данных, особенно если много выбросов. Среднее будет 0 и стандартное отклонение 1, хорошо подходит для нормального распределения данных. MinMaxScaler умещает масштаб данных в диапазон [0, 1]. Если их использовать до train_test_split, будет потеря данных. Тут надо следить, чтобы данные из val/test не попали в трейн.
from sklearn.model_selection import train_test_split X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.25, random_state=42) from sklearn.preprocessing import MinMaxScaler scaler = MinMaxScaler() X_train = pd.DataFrame(scaler.fit_transform(X_train), columns=X_train.columns) X_valid = pd.DataFrame(scaler.transform(X_valid), columns=X_valid.columns) |
Логистическая регрессия это про классификацию, поэтому в переменной Y должны быть значения 1 или 0. Accuracy это метрика оценки качества в задачах классификации, доля правильных ответов. Accuracy = (TN + TP)/(TN + TP + FN + FP).
from sklearn.metrics import accuracy_score clf = SVC(gamma=0.001, C=100.,verbose=True) import numpy as np clf.fit(X_train, y_train) |
y_pred = clf.predict(X_valid) y_pred_train = clf.predict(X_train) accuracy_score(y_valid, y_pred) from sklearn.linear_model import LogisticRegression lr = LogisticRegression(solver="lbfgs", penalty='l2') lr.fit(X_train, y_train) y_pred_train = lr.predict(X_train) accuracy_score(y_train, y_pred_train) |
Мы получили не самый удовлетворительный показатель accuracy = 0.6796407185628742, давайте улучшать. У модели SVC есть параметр C, который штрафует за ошибку классификации. По умолчанию этот параметр равен 1. Зададим несколько возможных значений для этого параметра и посмотрим, какие значения являются наиболее выгодными:
import numpy as np c_values = np.logspace(-2, 5, 36) accuracy_on_valid = [] accuracy_on_train = [] for i, value in enumerate(c_values): clf = SVC(C=value, kernel='rbf', gamma="auto") clf.fit(X_train, y_train) y_pred = clf.predict(X_valid) y_pred_train = clf.predict(X_train) acc_valid = accuracy_score(y_valid, y_pred) acc_train = accuracy_score(y_train, y_pred_train) if i % 5 == 0: print('C = {}'.format(value), '\tвалидационные = {}'.format(acc_valid)) print('C = {}'.format(value), '\tтренировочные = {}\n'.format(acc_train)) accuracy_on_valid.append(acc_valid) accuracy_on_train.append(acc_train) |
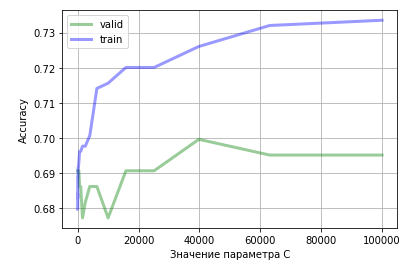
C = 0.01 валидационные = 0.6905829596412556 C = 0.01 тренировочные = 0.6796407185628742 C = 0.1 валидационные = 0.6905829596412556 C = 0.1 тренировочные = 0.6796407185628742 C = 1.0 валидационные = 0.6905829596412556 C = 1.0 тренировочные = 0.6796407185628742 C = 10.0 валидационные = 0.6905829596412556 C = 10.0 тренировочные = 0.6841317365269461 C = 100.0 валидационные = 0.6905829596412556 C = 100.0 тренировочные = 0.688622754491018 C = 1000.0 валидационные = 0.6860986547085202 C = 1000.0 тренировочные = 0.6961077844311377 C = 10000.0 валидационные = 0.6771300448430493 C = 10000.0 тренировочные = 0.7155688622754491 C = 100000.0 валидационные = 0.695067264573991 C = 100000.0 тренировочные = 0.7335329341317365
Как мы видим, точность на валидационных данных до определённого момента растёт. Начиная с 40 000 заметен спад точности на валидационных данных, однако, точность на тренировочных данных продолжает расти. Это означает, что модель начинает переобучаться.
import matplotlib.pyplot as plt plt.plot(c_values, accuracy_on_valid, label="valid", linewidth=3, alpha=0.4, color = "g") plt.plot(c_values, accuracy_on_train, label="train", linewidth=3, alpha=0.4, color = "b") plt.xlabel('Значение параметра C') plt.ylabel('Accuracy') plt.legend() plt.grid() plt.show() |
Помимо Accuracy, нужно учитывать F1, Precision и Recall. Если Accuracy = 86,43%, Precision =24,73%, то это неудовлетворительно. Точность низкая, модель нельзя внедрять. Всегда смотрим на матрицу ошибок.
Наглядно видно, как точность на валидационных данных при C=40000 уже выше, чем при использовании SVM без настройки параметров. Но следует понимать, что SVM не особо эффективен на шумных данных.

12 комментариев
Roman Kuncevich
Хорошая статья, спасибо! Куда посоветуете копать касательно прогнозов конверсии пользователя в платящего, отталкиваясь от цепочек событий?
Цветков Максим
Для начала обычно агрегируют данные о поведении. Еще можно векторизовать, смотреть в сторону RNN или LSTM с прогнозом временного ряда на несколько шагов в будущее. Еще хорошо работает ARMA и расширения этой модели.
Можно посмотреть и фундаментальный анализ (глубокое погружение в сферу), и технический аанализ (графики, свечи). Либо методы временных рядом, ARMA и ARIMA. Им на вход подается поведение графика и больше ничего, они счтывают закономерности и делают прогноз. Ну и любые типы регрессии, берутся все подсчитанные метрики и закидываются в систему. Сам временной ряд легко описывается трендом, частотой, амплитудой и временем.
Игорь Рыбкин
Максим, скажи куда копать по теме поиска зависимости между временем и действиями. Допустим, пользователь установил приложение и сделал действия, везде есть timestamp. Как понять зависимость корреляция между распределением действий во времени?
Цветков Максим
Я бы начал с G-test или табличного chi-squared test. И гуглить слово «коинтеграция».
Pavel Ivanov
Добрый день! есть график продаж по факту и модель предсказания, по графику они примерно похожи. По факту падение продаж куда больше, чем было по предсказанию. Как можно проверить, падение связано с какими-то факторами или модель предсказания кривая?
Цветков Максим
• Локализовать статистически значимое падение через доверительные интервалы на разных временных участках предсказания
• Построить модель на выявленном падении
• У нас есть модель во время падения и до падения, самое время сравнить коэффициенты моделей
Алексей Нагорский
что такое аномалия с точки зрения бизнеса?
Цветков Максим
Зависит от бизнеса. Просадка по деньгам — точно аномалия с точки зрения бизнеса.
Хорошо работают модели LightGBM quantile regression + BILSTM NN (Bidirectional LSTM). LightGBM отлично усредняет, дает меньше аномальных прогнозов. Если нейронка прогнозирует сильную аномалию, то мы этому не верим. Если в рамках некого окна, то верим. Для отсечения очень мощных выбросов из кластеров можно использовать DBSCAN.
Виктор
в каком инструменте можно собрать данные о ценах из разных РК?
Цветков Максим
Supermetrics, Owox. Также, из дорогих и стабильных решений, посмотрите fivetran/stitch. Supermetrics позволяет вытянуть данные из «Метрики» в Google Data Studio.
Бесплатно airbyte, но не обойтись без python+cron.
Alex Bodryk
Есть две выборки, одна похуже другая получше. Как оценить эффект различий между выборками?
Цветков Максим
Я бы смотрел в сторону Propensity Score Adjustment из медицины. Например, у вас две выборки — одна качественная вероятностная выборка, но маленькая. И вторая выборка это простая панель из интернета со смещениями. Вы можете смешать выборки алгоритмом, и получить вероятность принадлежности к эталонной выборке. Работает на основе соц. дема, географии, записанных активностей.